 |
|
Goniometrie
Autor: Mgr. Jiří Henzl
Definice funkcí y = sin x, y = cos x, y = tg x, y = cotg x pomocí jednotkové kružnice, vlastnosti těchto funkcí
Řešení goniometrických rovnic, orientace na jednotkové kružnici, geometrický význam funkcí y = sin x, y = cos x, y = tg x, y = cotg x
Užití sinové a kosinové věty, znění vět, případy použití
Aplikace goniometrických funkcí ostrého úhlu, definice jednotlivých goniometrických funkcí pomocí stran pravoúhlého trojúhelníku
Aplikace goniometrických vzorců, základní vzorce, součtové vzorce, vzorce argumentu 2x a x/2, vzorce pro součet a rozdíl hodnot goniometrických funkcí
Příklady
Určete, zda výraz je kladný, nebo záporný

Vypočtěte hodnoty všech goniometrických funkcí, je-li cos x = -1/8 a současně platí, že
x Î
<
p
, 3/2 p
>
Vypočtěte sin x a cos x , je-li tg x = -5/2 a současně platí, že x Î
<
3/2p
, 2p
>
Vypočtěte sin x, je-li tg x/2 = 2/3 a současně platí, že
x Î
<
0, p
/2 >
Řešte v R
2 sin2 x = tg x
Řešte v R
2 sin2 x = 3 cos x
Řešte v R
2 sin2 x - 3 cos2 x = 2 sin x
Řešte v R
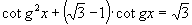
Vypočtěte vnitřní úhly trojúhelníku ABC, je-li a = 8, b = 8, c = 8 3
V trojúhelníku ABC nelze přímo změřit vzdálenost AB. Úhel ABC = 75°,
úhel BCA= 45°, BC = 150 m, AB = ?
Z místa A je vidět vrchol továrního komínu pod úhlem 35°, pata B komínu není přístupná. Z bodu B, který leží na přímce AP a je o 11 m blíž ke komínu než bod A je vrchol komínu vidět pod úhlem 49°.Vypočtěte výšku komínu.
Dvě síly o velikosti 72 N a 58 N působí v tomtéž bodě tělesa ve směrech, které spolu svírají úhel 72°. Vypočtěte velikost výslednice.
Na nakloněné rovině, jejíž stoupání je 30°, leží těleso hmotnosti 45 kg. Vypočtěte :
a) tlakovou a pohybovou složku tíhové síly tělesa
b) délku nakloněné roviny, v případě, že základna měří 27 m.
Výška kruhového mostního oblouku je 24 m a jeho rozpětí 82 m. Vypočtěte poloměr mostního oblouku a příslušný středový úhel.
Řeka široká 900 m teče přímo rychlostí proudu 2 m/s. Parník pluje kolmo na směr proudu rychlostí 4 m/s.
a) jaký úhel svírá dráha výsledného pohybu se směrem kolmým na proud ?
b) jakou rychlostí se parník pohybuje ?
c) jakou dráhu mezi břehy urazí ?
Dvě přímé ulice se křižují v místě K v úhlu 51°. Místo A na jedné z těchto ulic vzdálené od křižovatky 1625 m má být spojeno nejkratší cestou s druhou ulicí. Jak dlouhá bude tato spojka ?
Určete pro která x je definován výraz a upravte

upravte sin 750 - sin1350 (použijte součtové vzorce)
určete definiční obor

Dokažte

Dokažte

|
|
|
|
 |