      Martin Hozφk
      hozikm@seznam.cz
      ICQ: 323756613

Ovlßdßnφ autφΦka

Velk² poΦet Flashov²ch her je na motivy automobilov²ch zßvod∙. Zßkladnφm stavebnφm kamenem je samoz°ejm∞ auto. To se dnes nauΦφme ovlßdat.

Nejprve si vytvo°φme MovieClip, kter² bude p°edstavovat ovlßdanΘ auto a nazveme jej t°eba "car". Auto samoz°ejm∞ bude zobrazeno z ptaΦφ perspektivy.
MovieClipu "car" potΘ definujte vÜechny nßsledujφcφ p°φkazy:
Pou₧ijeme udßlost "Enter Frame". Ta znamenß, ₧e vÜechny p°φkazy uvnit° budou vykonßvßny v ka₧dΘm snφmku MovieClipu (i kdy₧ je t°eba jen jeden). Pro ty mΘn∞ chßpavΘ: p°φkazy se budou provßd∞t po°ßd dokola podle rychlosti framerate animace.

onClipEvent (enterFrame) {

Dßle vytvo°φme 2 hlavnφ podmφnky pro stisk levΘ a pravΘ Üipky. Po stisknutφ Üipky se automobil otoΦφ o urΦit² poΦet stup≥∙ a to zm∞nou atributu _rotation. Jeliko₧ otßΦφme MovieClip z n∞ho samΘho, nenφ t°eba psßt cestu (z hlavnφ osy by to muselo b²t takto: car._rotation). Pokud bychom ovlßdali tank, staΦilo by napsat jen ten jeden p°φkaz, my vÜak jezdφme s autem (v klidovΘm stavu se nem∙₧e otßΦet) a tak je t°eba p°idat jeÜt∞ podmφnky, kterΘ upravujφ rotaci podle rychlosti.

   if (Key.isDown(Key.LEFT)) {
          if (Math.abs(speed)>=0.2 & Math.abs(speed)<=1) {
                  _rotation -= 1;
          } else if (Math.abs(speed)>1 & Math.abs(speed)<=2) {
                  _rotation -= 2;
          } else if (Math.abs(speed)>2 & Math.abs(speed)<=3) {
                  _rotation -= 3;
          } else if (Math.abs(speed)>3) {
                  _rotation -= 6;
          }
   }

   if (Key.isDown(Key.RIGHT)) {
          if (Math.abs(speed)>=0.2 & Math.abs(speed)<=1) {
                  _rotation += 1;
          } else if (Math.abs(speed)>1 & Math.abs(speed)<=2) {
                  _rotation += 2;
          } else if (Math.abs(speed)>2 & Math.abs(speed)<=3) {
                  _rotation += 3;
          } else if (Math.abs(speed)>3) {
                  _rotation += 8;
          }
   }

DalÜφ podmφnka kontroluje stisk Üipek nahoru a dol∙ (zrychlovßnφ a br₧d∞nφ). Zde se po stisku pat°iΦnΘ Üipky bu∩ zv²Üφ nebo snφ₧φ hodnota prom∞nnΘ "speed". PovÜimn∞te si, ₧e kdy₧ prom∞nnß "speed" dosßhne 20, u₧ se dßl nezvyÜuje, stejn∞ tak, kdy₧ je rovna -10 (zpßteΦka), u₧ se dßl nesni₧uje.

   if (Key.isDown(Key.UP) & speed<20) {
                  speed += 1;
   } else if (Key.isDown(Key.DOWN) & speed>-10) {
                  speed -= 1;

Pokud bychom to nechali takto, auto by na neutrßl dr₧elo po°ßd svou rychlost. To je samoz°ejm∞ nereßlnΘ, a proto je nutnΘ, pokud nenφ zmßΦknut plyn (Üipka nahoru), postupn∞ sni₧ovat rychlost a₧ na nulu.

   } else {

             if (speed>0.5) {
                          speed -= 0.3;
             } else if (speed<-0.5) {
                          speed += 1;
             } else {
                          speed = 0;
             }
    }

Tak a nakonec jsme se dostali k tomu nejd∙le₧it∞jÜφmu, samotn² pohyb auta. Co nßsledujφcφ 4 °ßdky d∞lajφ? JednoduÜe m∞nφ ka₧d² snφmek pozici (_x a _y) MovieClipu "auto". Nechci vßm sahat do sv∞domφ, ale v∞°φm, ₧e n∞kterΘ z vßs polil studen² pot p°i pohledu na goniometrickΘ funkce sinus a cosinus. Pro ty mΘn∞ matematicky nadanΘ jsem proto nakreslil nßsledujφcφ obrßzek:

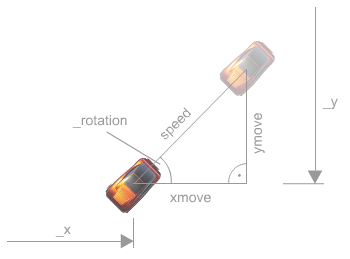
    xmove = Math.cos((_rotation-90)*(Math.PI/180))*speed;
    ymove = Math.sin((_rotation-90)*(Math.PI/180))*speed;
    _x += xmove;
    _y += ymove;

}

Vysv∞tlenφ pou₧it²ch goniometrick²ch funkcφ

Jak znßmo, sinus je v pravo·hlΘm troj·helnφku definovßn jako protilehlß odv∞sna ku p°epon∞ a cosinus jako p°ilehlß odv∞sna ku p°epon∞.

Snad jen dodßm, ₧e do goniometrick²ch funkcφ se ve Flashi ·hly dosazujφ v₧dy v radißnech. V jednotkovΘ kru₧nici platφ:

Poslednφ v∞c, kterou je t°eba ud∞lat, je p°iΦφst hodnoty xmove a ymove k sou°adnicφm _x a _y

P°φÜt∞ vßs nauΦφm, jak vytvo°it zßvodnφ drßhu, brzdicφ z≤ny s pφskem, st∞ny s pneumatik a dalÜφ.

prohlΘdnout

stßhnout [25 kB]