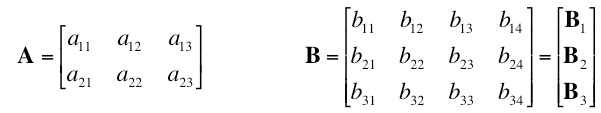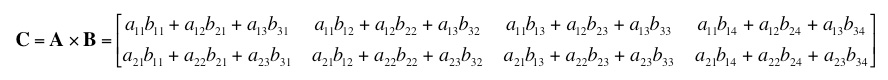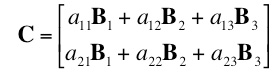Algorithms and Special Topics

Here you will find a series of tricks, tips and some perhaps non-obvious ways to micro-optimize code. In addition are also presented how to do a few common tasks like integer division, single precision floating point division and square roots. 

Division and Square Root (AltiVec)
Square Root and Reciprocal Square Root (Scalar)
Fast Floor (scalar)
Operating Across a Vector
The NaN method of Partial Vector Compares
Bit-wise NOR for NOT
Bit Counting
Byte Swapping
Type Conversions
Matrix Transpose
Matrix Multiplication
32x32 Bit Integer Multiplication
Load and Splat a Scalar
Note: Permute Naming Conventions

Division and Square Root (AltiVec)

AltiVec provides estimator instructions for both reciprocals and reciprocal square roots. To get the full precision reciprocal and reciprocal square root (within a few bits), you have to do one round of Newton-Raphson refinement. To get something that is close to the correctly rounded IEEE result (with a infrequent 1-2 ulp error), a second round of Newton-Raphson iteration is used using the result as the new estimate.

//result = a/b
inline vector float Divide( vector float a, vector float b )
{

return vec_madd( a, Reciprocal( b ), (vector float)(0) );

}

//result = v0.5
inline vector float SquareRoot( vector float v )
{

return vec_madd( v, ReciprocalSquareRoot( v ), (vector float)(0) );

}

//result = b-1
inline vector float Reciprocal( vector float v )
{

//Get the reciprocal estimate
vector float estimate = vec_re( v );

//One round of Newton-Raphson refinement
return vec_madd( vec_nmsub( estimate, v, (vector float) (1.0) ), estimate, estimate );

}

//result = v-0.5
inline vector float ReciprocalSquareRoot( vector float v )
{

//Get the square root reciprocal estimate
vector float zero = (vector float)(0);
vector float oneHalf = (vector float)(0.5);
vector float one = (vector float)(1.0);
vector float estimate = vec_rsqrte( v );

//One round of Newton-Raphson refinement
vector float estimateSquared = vec_madd( estimate, estimate, zero );
vector float halfEstimate = vec_madd( estimate, oneHalf, zero );
return vec_madd( vec_nmsub( v, estimateSquared, one ), halfEstimate, estimate );

}

Please note that these functions should not be considered IEEE-754 correct. Not only are they typically off by a few ulps, their edge case behavior may be very different. For example, division by zero may return a NaN instead of Inf.

Integer division is a bit trickier. There is no good way to either do integer division or generate an integer reciprocal directly. If you need to do these, the best thing to do is to use the VFPU to generate a reciprocal. In some cases, it is best to also do the following multiplication in the VFPU as A * (1/B), as the precision is greater. However, if you need to divide a series of integers by the same value and 12-15 bits of precision is enough, then in many cases you may find vec_mradds() to be better. Because this gives you 8-way parallelism, it is potentially twice as fast. In addition, you don't have to suffer the overhead of conversion to float and back. The following sample will divide an array of vector shorts by another vector short. We didn't bother with doing a Newton-Raphson optimization on the reciprocal because the extra three bits only survive the conversion to integer space if your input value is between -7 and 7. If you feel you need the added precision, then you can easily substitute the Reciprocal() function above, where vec_re() appears here:

inline void DivideArray( vector signed short *data, vector signed short divisor, int vectorCount )
{

//Calculate the signed 0.15 fixed point representation of the reciprocal of divisor
vector float fReciprocal1 = vec_re( vec_ctf( vec_unpackh( divisor ), 0 ));
vector float fReciprocal2 = vec_re( vec_ctf( vec_unpackl( divisor ), 0 ));
vector signed short reciprocal = vec_packs( vec_cts( fReciprocal1, 15), vec_cts( fReciprocal2, 15) );
vector signed short zero = vec_splat_s16(0);

//Multiply our data by the reciprocal
while( vectorCount--)
{

//vec_mradds does (( A * B + 2^14) >>15) + C, which
//is just right for 0.15 fixed point multiplication
data[0] = vec_mradds( data[0], reciprocal, zero );
data++;

}

}

Integer square roots are best done in the FPU.

Apple provides a suite of correctly rounded integer divides in vecLib.framework. These are available in signed and unsigned variants from 8 bit integers up to 1024 bit integers. See headers vBasicOps.h and vBigNum.h.

Square Root and Reciprocal Square Root (Scalar)

Those interested in square roots in the scalar domain would be happy to know that the techniques used for AltiVec above may be used there as well. The standard libm (a.k.a. MathLib) sqrt() function could be faster if you are willing to be a little bit sloppy with your calculations. The least significant bit from a Newton-Raphson result is often wrong, so Newton-Raphson can not be used to generate a IEEE result from fsqrte, but if you don't need that last bit, it could be used to generate a result that is perfectly fine for your application. Second, math.h specifies sqrt() return the square root of a single value. This calculation leaves the processor somewhat data starved. You can get much better performance if you write your own functions to do three square roots simultaneously, providing significant performance advantages. Best of all, you can tune the function to give you the best trade off between accuracy and speed. Please note that these functions are tune for the G3 and PowerPC 7400 and 7410, which have a 3 cycle FPU pipeline. For PowerPC 7450 and 7455, which have a five cycle FPU pipeline you may find some performance advantage to doing four or five square roots simultaneously.

If a zero is a possible input for inverse square root, then the algorithms described above should be modified as follows to avoid getting a NaN:

#if defined( __GNUC__ )
#include<ppc_intrinsics.h>
#endif

inline float FastScalarInvSqrt( float f )
{

float estimate, estimate2;
float oneHalf = 0.5f;
float one = oneHalf + oneHalf;

//Calculate a 5 bit starting estimate for the reciprocal sqrt
estimate = estimate2 = __frsqrte ( f );

//if you require less precision, you may reduce the number of loop iterations
estimate = estimate + oneHalf * estimate * ( one - f * estimate * estimate );
estimate = estimate + oneHalf * estimate * ( one - f * estimate * estimate );

return __fsels( -f, estimate2, estimate );

}

Fast Floor (Scalar)

AltiVec has a floor() instruction for floating point work, but frequently developers find they need a fast floor function for scalar code. While the libm floor function is very fast, there are code segments that would greatly benefit from being able to inline floor into inner loops. The following works for the default round to nearest FPU rounding mode on PowerPC for all values except for -0.0, for which it returns 0.0 instead of -0.0:

#if defined( __GNUC__ )
#include <ppc_intrinsics.h>
#endif

inline double fastfloor( double f )
{

double c = __fsel( f, -0x1.0p+52, 0x1.0p+52 );
double result = (f - c) + c;

#if 1

/* This case is likely a win for ordinary code */
if( f < result ) result -= 1.0;

#else

/* This case is probably a win for inlining into */
/* highly parallel/unrolled code */
result -= __fsel( f - result, 0.0, 1.0 );

#endif

return result;

}

Please note that some compilers may have difficulty scheduling __fsel() properly. It may be required that you unroll and inline by hand for optimal performance. We find the above code to be at least 2-3 times faster in our tests. For rounding modes that are not the default, the function produces identical output to floor over the range –2**105 ... 2 ** 105 (-4.05648e31 to 4.05648e31), except for -0.0 as noted above.

Operating across a vector

In general, you should try to always add among vectors, rather than across a single vector. However, in certain situations, it cannot be avoided. Here is the quickest way (we know of) to do this by type. Those based on vec_sums() return the result in the last cell. Those that use vec_sld will return the result in all cells. If you want to convert the former into the latter, use vec_splat().

Notice that when adding across a vector the hard way (as per vector float), it is not necessary to rotate one float and add each time. Rotate two, add then rotate one and add.

When you need to add across more than one vector, it can in some cases be more efficient to do a matrix transpose and add between the rows of the transposed matrix. You can even do the adding while you are doing the transpose, as the permute unit and the VALU can execute concurrently. This not only increases concurrent execution, but also reduces the number of permute instructions required as the each operation reduces the amount of data. It also gives you a result as a vector, rather than a scalar stored in a vector, making it more efficient to use downstream:

typedef vector unsigned int vUInt32;

//Comments show start cycle for execution on PPC 745x
vUInt32 AddAcross4( vUInt32 a, vUInt32 b, vUInt32 c, vUInt32 d )
{

vUInt32 tempA, tempB, tempC, tempD;

//First half of 4x4 a matrix transpose
tempA = vec_mergeh( a, c );//1 {a0, c0, a1, c1}
tempC = vec_mergel( a, c );//2 {a2, c2, a3, c3}
tempB = vec_mergeh( b, d );//3 {b0, d0, b1, d1}
tempD = vec_mergel( b, d );//4 {b2, d2, b3, d3}

//Add intermediate values
b = vec_add( tempA, tempC ); //4 {a0 + a2, c0 + c2, a1 + a3, c1 + c3}
d = vec_add( tempB, tempD ); //6 {b0 + b2, d0 + d2, b1 + b3, d1 + d3}

//Do half of the second half of the transpose
a = vec_mergeh( b, d ); //7 { a0 + a2, b0 + b2, c0 + c2, d0 + d2 }
c = vec_mergel( b, d ); //8 { a1 + a3, b1 + b3, c1 + c3, d1 + d3 }

//Find the result
return vec_add( a, c ); //10

}

While four calls to vec_sums finishes in seven cycles, rather than ten, you are left with the problem of how to efficiently use the result, which would be four largely empty vectors. 

The NaN Method for Partial Vector Compares

With proper planning, it is rarely necessary to do conditional tests on some but not all elements in a vector. However in rare circumstances it is unavoidable. When testing vector floats, there is a special trick one might use with NaN (Not a Number) to avoid testing some of the elements. The key is to notice that any test against a NaN always returns false. So, for example, if you want to determine whether both of the second or third elements are negative, you can test to see if they are less than { NaN, 0.0, 0.0, NaN }:

Boolean AreSecondAndThirdElementsBothNegative( vector float in )
{

#define QNaN 0x7FC00000
const vector unsigned int testData = (vector unsigned int)( QNaN, 0, 0, QNaN );
vector float test = vec_ld( 0, (float*) &testData );

return ! vec_any_ge( test, in );.

}

Bit-wise NOR for NOT

notX = vec_nor( x, x ); //returns ~x

In some cases vec_andc() (vector and with compliment) is appropriate instead.

Bit Counting

A small number of algorithms count the number of bits in a byte. This is usually done most quickly in the vector unit by using vec_perm to do a lookup table:

typedef vector unsigned char vUInt8;

vector unsigned char CountBits( vUInt8 v )
{

vUInt8 tab1 = (vUInt8) (0,1,1,2,1,2,2,3,1,2,2,3,2,3,3,4);
vUInt8 tab2 = vec_add(tab1, vec_splat_u8(1));
vUInt8 highBits = vec_sr(v, vec_splat_u8(5) );

return vec_add( vec_perm( tab1, tab2, v ), vec_perm( tab1, tab2, highBits ) );

}

The above function returns the number of 1 bits in each byte. Since the maximum result for any byte is 8, you can safely accumulate the byte results for 31 iterations before needing to accumulate the results into a larger integer. Accumulation into a larger integer type is probably most efficiently done using vec_sum4s. Shortly before returning you can use vec_sums to add across the accumulation vector used by vec_sum4s.

Byte Swapping

Another way to do it is to use XOR with a permute constant. In this case, create a identity permute with

identity = vec_lvsl(0, (int*) NULL );

Then XOR it with (vector unsigned char) (dataSize - 1):

byteSwapShorts = vec_xor( identity, vec_splat_u8(sizeof( short) - 1) );

byteSwapLongs = vec_xor( identity, vec_splat_u8(sizeof( long )- 1 ) );

byteSwapDoubles = vec_xor( identity, vec_splat_u8(sizeof( double ) - 1) );

byteSwapQuadwords = vec_xor( identity, vec_splat_u8(sizeof(vector float) - 1) );

This generates the appropriate permute constant to do the byte swap operation. You can also XOR the higher bits of the permute register to swap the orders that elements appear in a vector

Note that we have named each permute constant like a function. This is a handy convention for naming permute constants, which makes sense if one considers vec_perm to be a data driven function...

Type Conversion

Those above the arrows move the data type to the right along the conversion line. Those below the arrow, are for conversions that go from right to left.

Shorts and Longs

An example: Looking at conversions from vector char to vector short, we see vec_unpackh, vec_unpackl, vec_mergeh and vec_mergel. Both vec_unpack and vec_merge* have high and low variants because in the conversion of 16 chars to 16 shorts, we go from one vector to two. The high and low designation indicate whether to expand the first set of 8 or the second set of eight elements from the vector char into the vector short. Whether vec_unpack or vec_merge* is used depends on whether you want a signed (sign extended) or unsigned (zero extended) result. Vec_mergeh() is used with a vector full of zeros as the first argument.

In the short to char direction, there are three variants of vec_pack. Since conversion from a short to a char may overflow the char, we can handle the overflow using a modulo operation (vec_pack) or by saturating the value at the largest or smallest representable char (vec_packs or vec_packsu). The saturated conversions are available in signed and unsigned versions.

The conversions between vector short and long work similarly.

Pixels

32-bit to 16-bit pixel conversion is fairly straightforward in the 32->16 direction. The only caveat is that the least significant bit of the alpha channel propagates into the alpha bit in the 16-bit pixel, not the most significant bit. Things are less straightforward in the 16->32 bit direction, as the 5 bit color channel values from the 16-bit pixel end up in the low order five bits of the 32-bit pixel channels. A few rotates and an OR are required to do the complete conversion:

inline void Pixel16ToPixel32( vector pixel pixels, vector unsigned int *a, vector unsigned int *b )
{

vector unsigned char high, low;
vector unsigned char three = vec_splat_u8( 3 );
vector unsigned char two = vec_splat_u8( 2 );

high = (vector unsigned char) vec_unpackh( pixels );
low = (vector unsigned char) vec_unpackl( pixels );
*a = (vector unsigned int) vec_or( vec_sl( high, three ), vec_sr( high, two ) );
*b = (vector unsigned int) vec_or( vec_sl( low, three ), vec_sr( low, two ) );

}

Ints and Floats

Finally conversion between vector ints and vector floats is fairly straightforward. Each conversion function contains a literal five bit constant to indicate the position of the of the decimal point in the fixed point notation. Unfortunately, as there are 33 possible positions for the decimal and only 32 of them are representable in a 5 bit literal, one of them is missing. This is the one that you would need if you commonly use 0.32 fixed point notation.

Happily, conversion between ints and floating point can also be done using vec_madd() in many cases, so even if you have a strange fixed point format, the conversion can still be done. The basic conversion method is covered in the IBM PowerPC Compiler Writers Guide (p83). (The IEEE-754 floating point format is documented in a number of places, including the Motorola Programming Environments Manual for 32-bit Implementations of the PowerPC Architecture.) It is easily translated into the vector domain. Direct conversion from vector shorts and vector chars is possible with this general method, and in many cases can be faster than the more standard method. What is more, in some cases, you can fold an ensuing constant multiply add fused into the operation for free.

The following is a simple example that converts a 0.32 vector unsigned long to a vector float:

vector float Convert0_32FixedToFloat( vector unsigned int value )
{

vector float exponent = (vector float) ( 1.0 ); //0x3F800000
vector unsigned int nine = vec_splat_u32(9);
vector unsigned int significand;
vector float result;

//Right shift value so that it fits in the FP significand
significand = vec_sr( value, nine );

//OR it into the exponent
result = vec_or( exponent, (vector float) significand );

//Subtract the exponent back out.
return vec_sub( result, exponent );

//If you wanted to do a multiply add the result by two constants a and b, you could do that
// for free by replacing the subtraction with a vec_madd:
// a*(x-c) + b = a * x + k, where k = (b - a*c)

}

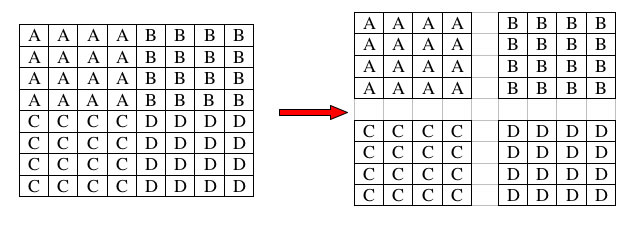
Please note that only the top 23 bits of precision in the 0.32 fixed point quantity are preserved with this method.

Matrix Transpose

As noted in the Code Optimization section, and elsewhere, matrix transposes are highly efficient tools to deal with interleaved data formats. Thus, their utility extends far beyond the small number of uses generally found in linear algebra. For example, you can easily turn 4 interleaved vectors:

struct{ float x; float y; float z; float w; }[4];

...into 4 uniform vectors:

vector float x;
vector float y;
vector float z;
vector float w;

... in 8 vector instructions. This second format is usually a lot easier to work with.

The general transpose algorithm is executed as a series of vec_merge(h/l)() instructions that interleave like rows above and below the vertical midpoint of the matrix. This is done iteratively to progressively reduce the height of the matrix by a factor of two each time, while at the same time doubling its width, until the matrix reaches dimension N² x 1. This array is the result. If you simply recast the array[N²] as a matrix[N][N], it is the matrix transpose of the input matrix.

The operation is represented graphically in this 8x8 example:

The method is fairly general for square matrices. Similar approaches can be used for rectangular matrices with some creativity. This method requires at least N+1 registers to do the transpose, though implementations that use 2N registers are common.

For large matrices, the best approach is to take a hybrid approach between simple scalar element swap algorithms and the vector merge approach suggested here. Block out the matrix into smaller chunks, each suitably sized for the merge algorithm. Load two complimentary chunks in, transpose them, then store each where the other came from.

For example, for an 8x8 matrix of floats, break the matrix down into 4 quadrants, each containing a 4x4 matrix:

The two quadrants along the diagonal (A and D) can be simply transposed in place. For B and C, load both into register, transpose each, then save B where C used to be and C where B used to be.

Matrix Multiplication

Sometimes in order to get an efficient vector implementation, one must approach a problem with a modified algorithm that does things in ways suitable for the vector unit. One example is matrix multiplication. The central problem facing would-be vectorizers for this task, is that using the traditional algorithm, rows of matrix A are multiplied by columns of matrix B, which may mean transposing matrix B. In addition you then have to sum across the result, which is not very efficient.

typedef vector unsigned short vUInt16;
typedef vector unsigned int vUInt32;

vUInt32 vec_mullw( vUInt32 A, vUInt32 B )
{

//Set up constants
vUInt32 sixteen = vec_splat_u32(-16);
vUInt32 zero = vec_splat_u32(0);
vUInt32 Bswap, lowProduct, highProduct;

//Do real work
Bswap = vec_rl( B, sixteen );
lowProduct = vec_mulo( (vUInt16)A,(vUInt16)B );
highProduct = vec_msum((vUInt16)A,(vUInt16)Bswap, zero);
highProduct = vec_sl( highProduct, sixteen );
return vec_add( lowProduct, highProduct );

}

Load and Splat a Scalar

Commonly when working with constant terms in vector code, it is desirable to be able to load a scalar and splat it across a register. Because the alignment of a scalar loaded into a vector register is generally not known at compile time, you can't simply use vec_splat. This can be done by rotating the data to a known position and then splat. In this case, we observe that splatting the permute map is the same as splatting the data, so we can use that to hide a bit of latency.

In this code example, the scalar being loaded must be naturally aligned. (e.g. a float must be 4 byte aligned.)

#define TYPE float
typedef vector unsigned char vUInt8;

vector TYPE vec_loadAndSplatScalar( TYPE *scalarPtr )
{

vUInt8 splatMap = vec_lvsl( 0, scalarPtr );
vector TYPE result = vec_lde( 0, scalarPtr );
splatMap = (vUInt8) vec_splat( (vector TYPE) splatMap, 0 );

return vec_perm( result, result, splatMap );

}

Note: Permute Naming Conventions

Permute operations can produce output that is hard to understand. This is true both because vec_perm is so flexible and also because fast permute constant generation schemes can be highly convoluted. It is suggested that you adopt a naming convention for permute constants that makes it clear what they do. Since each permute constant is actually a function stored as data, it may be appropriate to name the permute constant using function naming conventions. For example, "fixAlignment", "pivotMatrixColumn" and "reverseElementOrder" are a lot more informative than "permute1". Their use as the third argument of vec_perm() makes it clear what kind of data they are, and transfers their meaning to the vec_perm operation itself.

Table of ContentsNextPreviousTop of Page