Previous
TOC
Index
Next
| DirectX Media for Animation Media Types |
Previous |
TOC |
Index |
Next |
This section describes the abstract notion of image, geometry, and sound in Direct Animation and the operations on these types. There are operations (such as importing an image or 3D model) for constructing basic values in these types. There are other operations for constructing richly-attributed values such as producing a globe as a textured sphere. Still other operations create composite types such as combining sound and geometry into audible geometry.
The media abstractions provide a conceptual way to think of the media types, how they vary in relation to time, and the variety of operations on these types, without exposing any of the implementation details. This eases the construction of mixed media animations and enables interesting optimizations and a wide space of implementation possibilities.
In general, the way the abstractions are defined and the way they are implemented are quite different. The former is designed to facilitate thinking and reasoning about the media types while the latter is intended for maximizing performance while being as true as is feasible to the abstractions. This difference between abstraction and implementation is at the heart of the declarative approach in Direct Animation.
In this section we discuss the different media types separately and the interesting operations on these types. In the next section we discuss the mixed media operations across these types.
A value of the abstract type image has the following properties:
Each of the operations on images and attributes for images is described in terms of this abstract model. It is important to note that we use the term image in the broad sense to include an imported bit map, a rendered text, or a rendered triangle. All 2D geometric primitives are mapped into images, and can be thought of as constructors of images.
We will now discuss the image coordinate system, ways to construct images, and, later, the operations of the image type.
The image coordinate system is where images live and is, therefore, called the image plane. It has the following characteristics:
The following diagram demonstrates this coordinate system.

Note that all image and 2D geometric primitives live in this same continuous coordinate system. This includes all of the vector2, point2, transform2, path2, matte, text, montage, and image values and operations that are discussed below.
On its own, the image plane is of infinite extent, with an origin and X and Y-axes. Direct Animation images are constructed in this abstract coordinate system. However, when it is time to display a Direct Animation image, a certain section of the infinite plane is mapped on a region of a display device, as shown in the following figure.
The selection of the display region is up to the programmer and is outside the scope of Direct Animation. The mapping from the image plane into the display region is straightforward. The origin of the image plane is mapped to the center of the region, and then the mapping happens in like units of measure. For example, if there is a red point 2 CMS above the origin in the image plane, this point would map to a red pixel 2 CMS above the center of the display region. (Note that while commonly displayed regions are rectangular in shape, this is not necessarily the case with windowless Applets or ActiveX controls. Direct Animation intends to support such non-rectangular regions.)
If the author wants to view an image that maps outside the display region, then 2D transformations must be used to construct a new image that does fit within that region. For instance, if the author is interested in viewing the range (10,10) (15,15), he or she could construct two transformations. The first would translate this region's center (12.5,12.5) to the origin, and the second would scale the region to fit the display region. This is shown in the following example:
Transfrom2Bvr centeringXf = translate(toBvr(-12.5), toBvr(-12.5));
Transfrom2Bvr scalingXf = scale(div(viewportUpperRight.getX(), toBvr(2.5)),
div(viewportUpperRight.getY(), toBvr(2.5));
ImageBvr newImg = origImg.transform(compose(scalingXf, centeringXf));
Note that compose is a transform composition operation and transforms apply from right to left. In other words, the last expression above is equivalent to:
Imagebvr newImg = origImg.transform(centeringXf).transform(scalingXf);
There are several ways to construct values of the abstract image type. Once these values are constructed they are identical in terms of the operations that are applicable on them.
An emptyImage is the null image. As are all images, it is of infinite extent. It is also transparent and undetectable throughout.
A detectableEmptyImage is transparent and detectable throughout. An image is said to be tangible at a certain point if it is either detectable or non-transparent at that point. Otherwise, the point is said to be non-tangible. Also, see the cropping function described below.
Importation of Images
A basic way to construct images is through the importation of bitmaps represented in commonly used formats. This provides good leverage from the multitude of image authoring tools that currently exist. The form for importing an image is:
ImageBvr im = importImage("foo.jpg");
Direct Animation supports the importation of bitmaps in the .JPG, .GIF, and .BMP formats. The string reference to the image could be any valid URL. The obtained result is as follows:
Upon first reading, this may sound pedestrian. However, remember that the relationship between pixels and meters changes on a display-resolution by display-resolution basis. Thus, while one display may have a ratio of 18000 pixels per meter, another display may have a ratio of 22000:1. This means that the bounding box returned for an imported image varies depending on the specific display resolution. However, this is not true for all of the synthetic image constructors that we will discuss later in the document.
There are ways to work around the device-dependency of imported bit-maps. They involve scaling the bit-map in a device-dependent way so that the resultant image size is of some fixed, desired value across the different device resolutions. This topic is discussed in more detail in the section on mixed media. We will now discuss methods for constructing synthetic images.
One of the simplest images that can be constructed is a solid color image, as shown in the following example:
ImageBvr im = solidColorImage(color);
This results in an infinite-extent image with the color color behavior. Typically, such an image is either cropped or clipped (see image operations, discussed below), before it is used. Solid color images are commonly used to obtain solid-colored polygons or as viewport backgrounds, where the color can be time-varying.
Gradient fills provide a very compact form of interestingly colored images, where regions are filled with smoothly interpolated colors between specified colors at given vertices. The most general form of a gradient fill is obtained through the gradientPolygon(Point2s, Colors) method, which specifies an array of points and an array of colors. The arrays specify a triangular mesh with one color per vertex. The resultant image is based on a linear interpolation of the colors across each triangle in the RGB color model. Although interpolation in other color models may be desired, we map this CPU intensive operation to hardware, which currently only performs the interpolation in RGB.
Other more specialized forms of gradient fills, which are essentially shortcuts based on the general form described above, include:
Images can be constructed by rendering geometric 2D lines, as shown in the following example:
ImageBvr im = strokeImage(path, style, color);
In this example:
An attributed and colored version of the given path is rendered into an image according to the path's coordinates. Both path and style are abstract data types with their own operations for construction.
There is a shortcut to render a polyline into an image. It is:
ImageBvr im = polyline(numPts, points, color);
This avoids the steps of explicitly constructing a path and a style, where the path is simply the sequence of points. (The default line style has flat ends, beveled joins, dash solid, path not closed, and width of 2 points (.0076 meters or 2/72 inches).
Rendering Text:
Images can be constructed by rendering text, as shown in the following example:
ImageBvr im = text.render();
Here, text is of type TextBvr. This is an abstract type with attributes including font type, color, and style (bold or italic). A common constructor for text is simpleText, which takes a StringBvr and returns a TextBvr. For example:
simpleText(toBvr("any string"))
Also, toString is a method on NumberBvrs that converts the number to a StringBvr. The text, potentially attributed, is rendered into an image with its extent centered at the origin. By default, the text's color is black, its font family is serif proportional, and it is neither in bold nor italic. It will be the same size as the font that is used in the shell for title bars and other widgets. This means that the size will depend on the particular setting on the machine. See the section below on meter-based spaces to see how to render and scale the text into a resolution-independent size.
An example of rendering text and of the toString method is shown below:
TextBvr clockText = simpleText(localTime.toString(toBvr(0))). bold(). color(red). render(). transform(translate(posX, posY));
In this example, we construct a StringBvr of a time-varying integer based on localTime. From this, we construct a bold, red TextBvr and from this we obtain an image that we position appropriately.
Rendering Geometry
Images can be constructed by rendering geometry, as shown in the following example:
ImageBvr im = renderGeometry(geo, camera);
The details are in the next section on 3D geometry.
Using a Montage
An image can be the rendering of a montage, which consists of a list of ImageBvrs, each with a NumberBvr that indicates its Z-order in the list. As the Z NumberBvr changes with time, the order in which the images are composited changes accordingly. Montages are ideal for situations where the layering of the different images is dynamic.
The set of Direct Animation operations can generate new and more interesting images from given images. Also, some of these operations generate useful data such as bounding-box information about a given image.
Transformations
A transformed version of an image can be obtained by applying im.transform(xf), where xf is of type Transform2Bvr and can be an arbitrary 2D affine transform. The Transform2Bvr type has operations for constructing scales, translates, rotates, and shears from basic parameters such as NumberBvrs and Vector2Bvrs. It is also possible to construct transforms based on 2x3 matrices. There are additional operations to compose transforms, obtain their inverse, and check whether or not they are singular.
In the following example, we obtain a jumping rabbit from a rabbit sprite by using a behavior of type transform:
ImageBvr rabbit = importImage("rabbit.gif");
Transform2Bvr jumpTransform = ...; // some jumping reactive behavior
ImageBvr jumpingRabbit = rabbit.transform(jumpTransform);
Opacity
An image with a specific opacity, (which is potentially time-varying), can be obtained by applying im.opacity(opac) where opac is a NumberBvr. For opac 0 the resulting image is fully transparent, for opac ]0, 1[ the result is proportionally opaque, and for opac 1 the result is fully opaque.
Crop
Cropping is obtained by applying im.crop(lowLeftPt, upRightPt).This results in the tangible (either detectable or non-zero opacity) portion of the subject image that falls within the two given points of type Point2Bvr.
Tile
When applied to an image, im.tile(), tile infinitely replicates the image in all four directions. Typically, tile is followed either with a crop or a clip operation, or else it is used to generate the background of a viewport, and is, therefore, implicitly clipped while it is displayed.
Clip
Clipping is obtained by applying im.clip(matte), where matte is a MatteBvr. This is itself an abstract type with operations for constructing interesting matte regions. The resulting image is the portion of the original image that falls in the matte region and is otherwise transparent and undetectable.
A shortcut to clipping an image with a polygonal region is im.clipPolygon(num, points), which is a shorthand method for generating a polygonal matte and doing a clip.
Overlay
An overlay takes two images as parameters and returns an image that is made by overlaying the first image on top of the second. Blending takes place where the images overlap and are partially opaque. This is commonly referred to as alpha blending.
Miscellaneous methods:
The im.boundingBox() method returns the bounding box of the parts of the image that are tangible. This means either detectable or non-transparent. The im.undetectable() method returns the same image with its detectability channel set to false throughout.
A value of type geometry has the following properties:
Each of the operations on the geometry type and attributes for the geometry type is described in terms of this abstract model. We will now discuss the geometry coordinate system, ways to construct geometry, and, finally, the operations on geometry.
The geometry coordinate system is a right-handed, 3D coordinate system of infinite extent where geometric models are specified and transformed. The default unit of measure is the meter. It has an origin and X, Y, and Z-axes. The coordinate system is a right-handed one, as shown in the following drawing:
The following drawing illustrates the direction of positive rotation along an axis of rotation (the arrow points away from the origin):
Direct Animation geometric models are constructed in this abstract coordinate system. However, when it is time to display a model, a camera is needed to project the infinite space into an infinite plane, which is the image plane discussed in the section on images.
In other words, the 2D image plane is identical to the 3D projection plane. This is only reasonable because the result of projecting geometry via a camera is an image. The resulting abstract image is amenable to the same operations and rules as other images, including the display through a window.
The simplest way to construct geometry is by importing a geometry that is in either the .WRL or the .X format. This is done with importGeometry(URL). Another way to construct geometry is from lights, including ambient, directional, point, and spot lights. It is also possible to construct geometry from a sound source, which is used to give 3D spatial characteristics to a sound by embedding it in other geometric models. Finally, emptyGeometry is a constant of the GeometryBvr type and is vacuous throughout.
Two geometry values can be aggregated/combined into one via the union operation. Geometry can also be transformed using arbitrary 3D affine transforms.
Finally, geometry can be:
All of the above parameters can be time-varying.
Probably the most interesting operation on geometry is to render it with a camera and obtain an image in the image plane. Related operations include rendering it into a microphone to extract a sound, or into a pair of microphones to extract stereo sound.
The operation that constructs an image from a geometry is called render, and it takes both a geometry value and a camera value. The operation does a standard rendering/projection of the geometry by the camera using Direct3D as an underlying 3D API.
There are two cameras that are supported by Direct Animation. They are:
These cameras consist of the following three elements:
The cameras are constructed by the following methods:
public class CameraBvr extends Behavior {
public static CameraBvr perspectiveCamera(NumBvr n, NumBvr p);
public static CameraBvr parallelCamera(NumBvr n);
}
The parameter n is the distance of the near plane and the parameter p is the distance of the projection point along the +Z-axis in relation to the origin (that is, the image plane). Both n and p must be positive, and the near plane must be on the same side as the image plane in relation to the projection point. A runtime error will result if this is not the case.
Both n and p can be time-varying because they are NumBvr. This is convenient for changing camera parameters. For example, varying p changes the perspective effect. Additionally, n can be made to vary with p. The distance of the near plane to the projection point is typically a fixed fraction of the range of dwelling of the geometry (this is where the geometry should reside to avoid clipping). Also, the choice of the near clipping plane must be tempered by Z-buffer resolution issues. (This is discussed later in the document.) A camera can be attributed by a far clipping plane as well. This is primarily for the same Z-buffer resolution issues.
Rendering involves projecting the geometry that resides on the opposite side of the near plane, in relation to the projection point, into an image on the image plane. The resultant image is infinite in extent, and, if the author is interested in only a section of it, the author must use 2D operations such as crop or clip on the image to extract that section.
Direct Animation cameras have an origin at [0,0,0] and can be transformed using standard Transform3Bvr values. Note that such transformations affect the placement of the projection point, the near plane, and the image plane. Translation and rotation can be used for positioning the camera relative to the geometric model being projected.
The X and Y scales can be used to zoom in or out in relation to the rendered model. Increasing the XY scale results in a zoom out (the rendered image shrinks), while decreasing the XY scale results in a zoom in (the rendered image grows). Controlling the perspective effect is achieved by changing p. The closer the projection point is to the projected object, the more pronounced is the perspective effect.
The rendering engine determines a far plane that is parallel to the near plane, at the furthest point, in relation to the near plane, of the model being viewed. The media engine then formulates a camera projection transform that maps the space between the near plane and the far plane into the available Z buffer resolution, which, in the case of Direct3D, is 16 bits. This has two ramifications:
The following figure shows reverse Z-mappings, where equal Z-units of distance in display coordinates (post-viewing) are mapped into markers on a Z-axis in world coordinates (pre-viewing). The figure also shows the impact on the Z-resolution of moving the near plane closer to the projection point.

For the user to bound Z-resolution, we provide a far-plane attribute (which means it is an optional parameter) that can be applied to cameras. A programmer, by specifying this attribute, would be explicitly indicating that objects beyond a certain distance in relation to the near plane would get clipped. Effectively, this attribute is a means for programmers to place a bound on the minimal Z resolution, measured in meters, in the range of interest. Actually, an alternative way to specify this attribute is also provided. This is by directly specifying a bound on the Z resolution, and having the system select the far clipping plane accordingly.
A value of type sound has the following properties:
Each of the operations on sound and attributes for sound are described in terms of this abstract model. We will first discuss ways to construct sound, and then the operations on sound.
A common way to construct sound is by importation from a file representation, through importSound(URL, length), in the .WAV and .MIDI formats. Upon importation, the length of the imported sound, in seconds, is returned as the length parameter. The sinSynth value is a sine wave based sound, which, when attributed (see the next section) can be the basis of a diverse set of synthetically generated sound waves. Furthermore, silence is a constant of SoundBvr type that is vacuous throughout. Other ways to construct sound is by rendering geometry with embedded sound into a microphone for a single channel sound and into two microphones for stereo sound.
For best results with .WAV files we propose a canonical format with a mono-sound used at a sampling rate of 22050Hz, which is half of 44100Hz (this is the rate of an audio CD), and a dynamic range of 16-bits. Importation of stereo-sound, a variety of sampling rates, and dynamic ranges of 8-bits and 32-bit floats is also supported. The canonical format strikes a balance between the quality of sound and some implementation pragmatics.
New sounds can be obtained from seed sounds using parameters and operations. The loop method takes a sound and repeats it forever. The gain method scales the amplitude of the sound wave by a specified scalar. The rate method scales the time dimension of the wave, effectively squeezing or stretching the sound wave. Modifying the rate is equivalent to time-transforming sound by a scalar multiplication function. The phase method shifts the sound wave by a specified parameter. For positive phase values, the sound starts with silence for the specified amount of time before the sound wave begins, and for negative values the corresponding front part of the sound wave is skipped. The parameters to gain, rate, and phase are themselves reactive numbers, and could be (and typically are) time-varying. For example, it is common to relate a distance between a moving sound source, such as a squeaking bird, and a listener, by using the gain parameter.
Pan
The pan method takes a stereo sound and scales the gain of the left and right channels according to a pan parameter, panAmt. It works as follows:
Gain
Direct Animation supports 16-bit sound and expects all sounds to be normalized. This means that, for maximum resolution, all 16 bits are used. A consequence of this is that all sounds seem equally loud. For example, a jet plane and a whisper will sound as though they are the same volume.
To rectify this, sounds are pre-scaled with the gain method. Because there is no way to change the actual gain of a PC's amplifier, sounds can only be attenuated. Attenuating a sound is the same as multiplying it by a value between 0 and 1.
In the next example, the two sounds, which are heard in the left and right channels respectively, will have an equal volume, even though their gains are different:
SoundBvr snd1 = importSound("...", null);
setSound( mix(
snd1.gain( toBvr( 1 ) ).pan( toBvr( -1 ) ),
snd1.gain( toBvr( 5 ) ).pan( toBvr( 1 ) ) ) );
In other words, the gain is clamped at one. The next example makes the sound in the left channel louder than the sound in the right channel:
setSound(mix( snd1.gain(toBvr(1)).pan(toBvr(-1)), snd1.gain(toBvr(0.2)).pan(toBvr(1))));
When sounds are embedded in a geometry and spatialized (using GeometryBvr.soundSource and a MicrophoneBvr), then gains larger than 1 can be used to allow the sounds to be heard from farther away than sounds without the scaling factor.
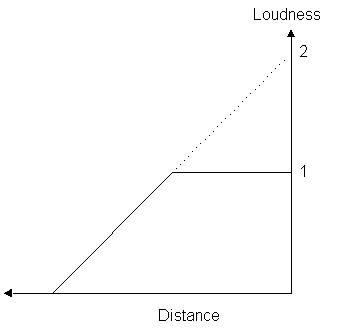
In particular, loud sounds such as a jet engine should be scaled by a gain > 1. However, unlike sounds in the real world, the sound will only become louder as you approach until the gain is equal to 1. Once this limit is reached, there is no more attenuation, and the sound's volume remains constant no matter how much closer you come.
The following diagram relates distance to a gain of 1 in an approximately linear fashion:

The next diagram shows how, for gains larger than 1, the volume is clamped at 1.
Mix
The mix method merges two sound waves into one by adding the corresponding waves. The common implementation of mixing is to add corresponding wave samples, and it is implementation-dependent how two imported sounds of different sampling rates and/or different bit depths are mixed together. In the case of an overflow of values while mixing, the result is clamped to the highest possible value.
The operations provided by Direct Animation on SndBvrs allow the generation of rich synthetic sounds from basic sound seeds by parameterization and layering (or mixing). The idea is to attribute the seed sounds with animation-related or random parameters that are usually time-varying, and then to mix the results together in a fashion consistent with the animation. This process is not very different from what is commonly done with 3D models. Simple parts are transformed, colored, or textured and then combined together into more interesting models. This means sound can be as flexibly and synthetically generated as 3D models are.
For example, in the Lighthouse sample included in the SDK, this technique is used to generate the ocean ambient sound, which is parameterized by the weather condition parameter, which, in turn, is controlled by the slider. Two constructs are used for the layering and parameterization of sound in Lighthouse that are generally useful. One is for generating parameterized cyclic sounds and the other for generating parameterized and random periodic sounds (the latter has a silence period between the different occurrences).
![]()
© 1997 Microsoft Corporation. All rights reserved. Legal Notices.