|
|
Dark Matter
Try this!
Picture a rocket being launched into space. How fast do you think it must travel to escape the earth's gravitational pull? You can determine this by using the escape velocity equation,
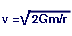
with m as the mass of the earth and r
as the radius of the earth. Calculate how fast the rocket must travel
to escape from the earth.
Is it:
- 5 km/sec
- 8 km/sec
- 11 km/sec
How does this apply to dark matter? One of the most important uses of
X-ray observations of clusters of galaxies has been the determination of
mass estimates for these systems.
The fundamental assumption is that the hot, X-ray emitting gas between the
galaxies in the cluster is trapped in the gravitational well of the cluster
and roughly in hydrostatic equilibrium. Both of these assumptions have
been shown to be fair, based on the observational measurements to date.
The X-ray observations from satellites such as ROSAT and ASCA can be used
to determine the gas density profile and temperature. These values are
then fed into a mathematical model to determine the total mass of the
cluster. This value can then be compared to the observed luminous mass
(i.e., mass of galaxies plus hot gas as determined from visible light
observations).
Think About!
If the hot gas is observed to be moving at an average velocity of
18,600 km/sec and still remain gravitationally bound to the cluster of
galaxies, how much mass must be attracting it? The radial extent of
the cluster is 300 kiloparsecs.
Compare your result to the observed luminous mass of 2 x 1012
solar masses. The difference in mass is due to dark matter, that is,
non-luminous mass. What percentage of the galaxy we have been working
with (NGC2300) must be composed of dark matter?
This activity was developed by Jacqueline Slay, Largo High School, Largo, MD
|
