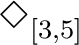MTL — hidden clock linear logics and other RTTL fragments

Metric Temporal Logic (MTL) [64] is a fragment of RTTL in which references to time are restricted to bounds on the temporal operators. For example, the formula A→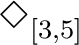B means that if A occurs then eventually within 5 time units B must occur. No references to an explicit clock are allowed and hence MTL is called a hidden clock or bounded temporal operator logic.

Interpretations for MTL are metric point structures based on a linearly ordered time domain. A distance function provides a metric for time. Various time constraints can be imposed on the distance function, depending on the notion of time that is used (e.g. transitivity, irreflexibility, and the existence of absolute differences).

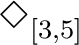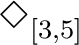In the hidden clock approach, is a new temporal operator that restricts or bounds the scope of the qualitative operator . The bounded formula B predicts the occurrence of B within 5 time units from now. The qualitative formula B asserts that B will eventually happen, but puts no bound on when.

In [64], a real-valued time domain is used. This allows MTL to express certain properties of continuous time variables (e.g temperature and pressure) more succinctly than discrete time logics. MTL does not allow references to an absolute point in time, nor does it allow the specifier to relate adjacent temporal contexts. A sound proof system for MTL is provided.

An important extension to the literature on MTL is a compositional proof system for Occam style programs [52,50]. The proof system uses the maximal parallelism model of program execution . Because the proof system is compositional, the properties of a compound system P₁| P₂ (the parallel composition of two simpler processes P1 and P₂) can be deduced from specifications of its constituent parts (P₁ and P₂), without any further information about the internal structure of these parts. Compositionality is important for scaling up the application of the proof system to deal with large systems in a structured fashion.

It is not clear whether the proof system can be extended to reason about complex plant descriptions, which are not always representable in Occam. The extra chop operator, needed for compositional proofs, makes the reasoning relatively complex. Nevertheless, once a module's specification is fixed, any implementation of the module with the same specification can be used, without having to redo the proof.

Alur and Henzinger [6] have compared various ways in which to restrict RTTL to obtain decidable fragments of the logic. These fragments are restricted to finite state, propositional temporal properties. There are at least four interesting syntactic fragments of RTTL:

• MTL [7,64] is a discrete time propositional version of the bounded operator logic discussed above.

• XCTL [43] is a discrete time propositional explicit clock logic. The atomic timing constraints allows the primitives of comparison and addition. XCTL restricts the quantification level. It allows only one outermost level of quantification over rigid time variables. The quantification is therefore never explicitly displayed. On the other hand, it allows general arithmetic timing expressions, including addition and subtraction of variables and constants.

• TPTL [7] is a discrete time propositional logic whose timing constraints allow comparison and addition (but only of integer constants, i.e. no variables). TPTL uses auxiliary static timing variables to record the value of the clock at different states, but replaces the explicit references to the clock itself by a special type of freezing quantification.

• MITL [5] employs a dense time domain. It has a bounded-operator syntax, but cannot express punctuality properties. A punctuality property states that the event B follows A in exactly 3 seconds.

All of the above fragments can be interpreted over discrete, dense and continuous time domains. The fragments can then be compared for expressiveness, and complexity of satisfiability and model-checking.

Satisfiability is important in the homogeneous verification case. Let the implementation I and the specification S (that the implementation must satisfy) can both be given as temporal logic formulas F_I and F_S respectively, in the appropriate fragment of RTTL. Then the implementation I meets the specification S iff the implication F_I→F_S is valid (or, equivalently, if the conjunction F_I∧¬F_S is unsatisfiable). Only propositional versions of temporal logics are decidable for satisfiability. Decidability depends on the nature of the time domain (discrete, dense etc.) and the operations on the time domain that are permitted.

Model checking is important in the heterogenous verification case. The implementation I is given by a timed automaton or timed transition system [4,5] A_I. The specification S is given by a temporal logic formula F_S. To do the check, a timed automaton A_¬FS is constructed from the negation of the specification ¬F_S. The implementation I satisfies the specification S precisely when the product automaton A_I×A_¬FS has no run (timed observation sequence).

Let RTTL(<,s) denote the restriction of RTTL to propositions and timing constraints containing only ordering (<), successor(s), and congruence over time (e.g. all times with an even time difference from the initial state). Thus, RTTL(<,s) is interpreted over a discrete time domain, and can be used to specify constant lower and upper time bounds on the time distance between events. The various logics are compared in Table  for satisfiability, model checking and expressiveness over discrete and dense time domains relative to RTTL.

For any real-time logic that is closed under boolean operations, and that can express punctuality, the satisfiability problem is undecidable for a dense time domain. MITL cannot express punctuality properties, and is thus less expressive than the other logics, but remains decidable even if the time domain is dense.

In [43] it is shown that XCTL and TPTL/MTL are incomparable. For each of these logics, there is a property expressible in one which is not expressible in the other. Each of these properties is a reasonable real-time requirement. In the discrete time case, TPTL and MTL are equally expressive (it is conjectured that this equality does not extend to dense domains [46]).

There are doubly-exponential-time decision procedures for both TPTL and MTL. The verification algorithm for MTL depends, exponentially, on the value of the largest time constant involved. It is a little less expensive than the algorithm for TPTL, which depends exponentially on the value of the product of all time constants.

XCTL is not closed under negation, and hence cannot be used to solve the homogeneous verification problem. However, a special model-checking algorithm for XCTL has been given that is doubly exponential in the size of the specification formula and singly exponential in the size of the model.