Funny thing, every time I have been interviewed for a game programming job, I've been asked to write
out longhand a line drawing algo. I've watched the people I was being tested with fumble over
this one for a while and then quietly asked "do you want me to write all the special cases, too?" The
point I'm making is that line drawing is one of those things you're going to need to learn just so
you can say you know it. Thought that you could avoid that kind of thing by being a coder, eh? HAR
HAR HAR! *actually falls down he's laughing so hard*
Note: For the remainder of this tutorial the following values will be used:
- pBuf: a pointer to the buffer to write to
- bWidth: the buffer width, in pixels
- bHeight: the buffer height, in pixels
- Ax, Ay: the starting coordinates of the line (whole numbers)
- Bx, By: the ending coordinates of the line (whole numbers)
It is also assumed that the buffer is a single contiguous block of memory begining in the top left
corner and moving left to right, top to bottom.
Line drawing can be as simple or as complicated as you want it to be. Let's start with a few
fundamentals. The first thing we can do is simplify our problem by only drawing from left to right.
if( Ax > Bx ) {
int c;
c = Ax;
Ax = Bx;
Bx = c;
c = Ay;
Ay = By;
By = c;
}
Not to hard and it means we only need to consider a few cases.

So the cases are:
- y=0 (horizontal line)
- x=0, y=+/-n (vertical lines)
- x=y, x=-y (diagonal lines)
- x > | y | (between x=y and x=-y)
- | y | > x (everything else, duh)
Do you see why there are 4 special cases? It all has to do with the slope of the line. As long as you
remember "slope of the line, slope of the line" (if you build it, they will come) you can derive all of
this stuff over again.
Case 1: y = 0
pBuf += Ay * bWidth + Ax;
for( int i = Ax; i <= Bx; i++ ) *pBuf++ = pixelColor;
OOH, that was so big and scary, wasn't it boys and girls? (Wallace, stop poking Suzie.
And while you're at it, stop touching her, too.)
Case 2: x = 0
int dir;
if( Ay > By ) {
int c;
c = Ay;
Ay = By;
By = c;
dir = -bWidth;
} else dir = bWidth;
pBuf += Ay * bWidth + Ax;
for( int i = Ay; i <= By; i++ ) {
*pBuf = pixelColor;
pBuf += dir;
}
Case 3: x = | y |
int dir;
dir = Ay < By ? bWidth : -bWidth;
pBuf += Ay * bWidth + Ax;
for( int i = Ax; i <= Bx; i++ ) {
*pBuf = pixelColor;
pBuf += 1 + dir;
}
Talk about a shocking difference, hey what? This time I took the if statement out of the loop so as to gain (a
small) speed boost. Anywhere you can gain a speed boost without making your code too confusing, go for it.
Mheh, must have more ...SPEED.
For those of you have have never seen the version of if then else written as ( case ? true : false ), well,
it's real code, it will run. Not that I reccomend it.
Case 4: x > | y |
double slope, counter;
int dir;
counter = 0.0;
slope = abs( By - Ay ) / ( Bx - Ax );
dir = Ay < By ? bWidth : -bWidth;
pBuf += Ay * bWidth + Ax;
for( int i = Ax; i <= Bx; i++ ) {
*pBuf = pixelColor;
pBuf++;
counter += slope;
if( counter >= 1.0 ) {
counter -= 1.0;
pBuf += dir;
}
}
Let's break that down and see what it does:
- Move the pBuf pointer to the start of the line.
- Find the slope of the line, that is to say the change in y vs. the change in x.
We want this because line line move more in the x direction than the y direction.
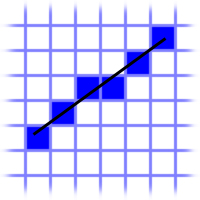
If the change in x were more than the change in y then we'd want to draw a certain number of pixels in
a horizontal line, move in the y direction by 1 and then repeat until we get to the end. But how often
do we move in the y direction? Put another way, how many pixels do we draw before we move up or down?
The slope of the line is the key. Think about it: when the line is horizontal, the slope is 0 (there
is no change in x) so we just draw a straight line. When the line is diagonal, the slope is 1 so y is
incremented every loop, at the same speed as x. So in between x=0 and x=y it's the slope of the line
that tells us when to move in the y direction. Why? Because we're looking for (y/x)*n >= 1.
Remember: the slope (y/x) will ALWAYS be less than 1 in this case.
- Loop for the x length of the line. Every time through the loop increment x and add to a counter the
slope. When the counter reaches 1, subtract 1 and move in the y direction.
Case 5: | y | > x
int counter, dy, dx, dir;
counter = 0;
dx = Bx - Ax;
dy = abs( Ay - By );
dir = Ay < By ? bWidth : -bWidth;
pBuf += Ay * bWidth + Ax;
for( int i = 0; i <= dy; i++ ) {
*pBuf = pixelColor;
pBuf += dir;
counter += dx;
if( counter >= dy ) {
counter -= dy;
pBuf++;
}
}
- Move the pBuf pointer to the start of the line.
- Find the inverse slope of the line, that is to say the change in x vs. the change in y.
We want this because y changes faster than x.
- loop for the y length of the line. Increment y every step, increment x when appropriate.
There was only one more optimization I could make and that was to remove all the
doubles from the loops. Why did this work? In case 4 we were looking for
(A/B)*N >= 1, when I didn't know what N was. In case 5 I rearranged the variables so that I was
looking for A*N >= B which is the same thing but it dosen't require a floating point number so not only
is it faster but it's guaranteed to be more accurate out somewhere near the 12th decimal place (:
You can and should do this same thing for both case 4 and case 5, I did it this way to smooth the
learning curve.
Now, just for the sake of argument, you could make a single loop to do all the different kinds
of line drawing. It wouldn't be as fast and it'd be a lot harder to read, but it would run. First of
all, you'd need to separate the x and y components as suggested earlier. Then before the loop you'd
have to set up everything in generic terms like a and b instead of x and y. You'd also need an
incrementA and incrementB so that
while( counter >= db ) {
counter -= db;
pBuf += incrementA;
}
Some tips for debugging your line drawing functions:
- Test each case. I drew each of the following lines one at a time on the screen in 32 bit color depth.
#define MAKECOLOR32( x, y, z ) ( ( x << 16 ) + ( y << 8 ) + ( z ) )
Line(5, 105, 5, 5, MAKECOLOR32( 0xff, 0x00, 0x00 ) ); // red
Line(5, 105, 55, 5, MAKECOLOR32( 0x00, 0xff, 0x00 ) ); // green
Line(5, 105, 105, 5, MAKECOLOR32( 0x00, 0x00, 0xff ) ); // blue
Line(5, 105, 105, 55, MAKECOLOR32( 0xff, 0xff, 0x00 ) ); // yellow
Line(5, 105, 105, 105, MAKECOLOR32( 0xff, 0x00, 0xff ) ); // purple
Line(5, 105, 105, 155, MAKECOLOR32( 0x00, 0xff, 0xff ) ); // aqua
Line(5, 105, 105, 205, MAKECOLOR32( 0xff, 0xff, 0xff ) ); // white
Line(5, 105, 55, 205, MAKECOLOR32( 0xaa, 0xaa, 0xaa ) ); // grey 1
Line(5, 105, 5, 205, MAKECOLOR32( 0x55, 0x55, 0x55 ) ); // grey 2
- If you don't separate the dx and dy variables in case 5, make sure that your
for() loop goes from 0 to
<= abs( dy ) or else
you will be unable to draw lines that slope sharply upwards.
- If you don't separate the dx and dy variables and your slope calculation is returning zero it's
because you have a compiler that employs strict typecasting. You need to calculate the slope as
slope = (double)abs( By - Ay ) / (double)( Bx - Ax );
That covers all your basic line drawing needs...provided you don't need to clip to screen dimensions, or
draw a line of thickness greater than 1, or antialias the line, or draw a curved line, or use
coordinates that are floating point numbers or a hundred other things...
Back to the top
NEXT: Line clipping
|