One of the largest problems when rendering large polygon sets has to do with the order in which the
polygons are supposed to be drawn. What I mean is that you have to have a really fast way of sorting
the polygons so that you can draw the polygons closest to the camera on top of the polygons that are
further back. Better still would be to have zero overdraw, by that I mean you wouldn't draw
over anything and every pixel would be touched just once.


There are a number of different ways of going about polygon sorting. Some of simplest include
the Painter's algorithm and Z-buffering. Portals are (among other things) another very handy way to
ensure front to back zero overdraw but we'll discuss those later.
Binary Space Partitioning trees (BSPs) are very good at a number of things.
- Z-sorting polygons so that they draw in the right order.
- Collision detection against BSP planes is very quick and easy. It's just as easy to
determine if you are inside our outside of a model represented by BSP.
- Fast rendering can be quickly accomplished because the BSP is built ahead of time. For those
of you mathematically inclined, the total time to walk the tree is O(n) while the time to build the
tree is O(n2).
- Node clipping is another precalculated BSP trick to improve rendering speed.
- The Possible Visible Set can be calculated with the BSP tree to reduce rendering time even
further.
If that isn't enough to convince you of the advantages, then maybe this is:
All of these programs use BSPs. "So how," you're asking yourself, "do I jump on the BSP bandwagon?"
Easier said than done.
First of all, here's how they work: BSPs "recursively divide space into pairs of sub spaces, each
separated by a plane of arbitrary orientation and position."1 It's easier to visualize.
Let's say we're given an arbitrary set of polygons. We'll use the planes of the polygons to cut the
world in half, or as close to half as we can find. The first step would look like this:
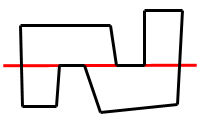
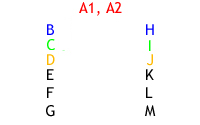
Recurse on both sides until there are no polygons left.
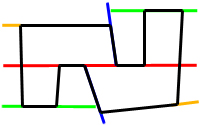
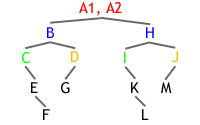
This is what is referred to as node-based because the polygons are on the nodes. The other type
of tree is a leaf-based tree and looks like this:


Notice a few important things:
- In both cases every node obtained a plane from a polygon. This isn't
strictly crucial, but it's a lot faster than trying to find an arbitrary plane.
- The area in front of and behind every node is a convex space. This will come in handy later.
- The front portion of every LEAF NODE is of a finite volume. This too, will be very useful later.
- If the best dividing plane cuts through a polygon, the polygon is cut in half and each half is then
used in the appropriate recursion.
Now that's all well and good, but how do you code it? Tsk tsk. That will be your homework for the
weekend, which is about how long it took me to write my first BSP building METHOD. No, I Jest. here's
some code for building the node-based BSP tree from a set of polygons.
/* BuildTree( cPolygon *pList )
* Given a linked list of polygons BuildTree finds the
* best dividing plane and then cuts the entire set
* based on that plane. If there is anything left in
* either half, the function recurses "down" that
* branch of the tree. Returns a success code.
*/
eNodeReturn cNode::BuildTree( cPolygon *pList ) {
cPolygon *pBestDivider, *pTest,
*pInsideList, *pOutsideList;
pInsideList = NULL;
pOutsideList = NULL;
pBestDivider = FindBestDivider( pList );
// pPlane is a member of cNode.
pPlane = pBestDivider->GetPlane();
for( pTest = pList; pTest; pTest = pTest->Next() ) {
// Test each polygon against the plane
// and put them in the appropriate list.
switch( pTest->TestAgainstPlane( pPlane ) ) {
case ZV_PLANE_BACK:
if( !pInsideList ) pInsideList = pTest;
else pTest->Link( pInsideList );
break;
case ZV_PLANE_FRONT:
if( !pOutsideList ) pOutsideList = pTest;
else pTest->Link( pOutsideList );
break;
case ZV_PLANE_ON:
// pPolygons is a member of cNode.
if( !pPolygons ) pPolygons = pTest;
else pTest->Link( pPolygons );
break;
case ZV_PLANE_SPLIT:
cPolygon *pIn, *pOut;
pTest->Split( pPlane, & pIn, & pOut );
// check to make sure Split succeeded
delete pTest;
if( !pInsideList ) pInsideList = pIn;
else pIn->Link( pInsideList );
if( !pOutsideList ) pOutsideList = pOut;
else pOut->Link( pOutsideList );
break;
}
}
// Recurse, if necessary.
// pInside and pOutside are members of cNode.
if( pInsideList ) {
pInside = new cNode();
// check to see if pInside exists
pInside->BuildTree( pInsideList );
// check to make sure BuildTree succeeded
}
if( pOutsideList ) {
pOutside = new cNode();
// check to see if pOutside exists
pOutside>BuildTree( pOutsideList );
// check to make sure BuildTree succeeded
}
return ZV_NODE_OK;
}
Thought that was rough? The first time is always the worst. Nowadays I
can do this in my sleep and I'm sure you will too in no time at all. Of course, you still have to
fill in the blanks and that, as they say, is another story. But it's going to be worth it, oh yes!
Let me show you just how easy it is to render using BSPs.
/* RenderTree( pCamera *pCam )
* Recursively calls all the nodes in the tree
* and renders them. The tree is "walked" from
* back to front to ensure proper polygon ordering.
* This method will work with both leaf and node
* based trees.
*/
void cNode::RenderTree( cCamera *pCam ) {
int result;
result = ClipToCamera( pCam );
if( result == ZV_NODE_CULLED ) return;
switch( result pCam ) {
case ZV_NODE_FRONT:
// Camera is in front of this node's plane
pOutside->RenderTree( pCam );
RenderNode( pCam ); // render this node's polygons
pInside->RenderTree( pCam );
break;
case ZV_NODE_BACK:
// Camera is behind this node's plane
pInside->RenderTree( pCam );
RenderNode( pCam ); // render this node's polygons
pOutside->RenderTree( pCam );
break;
}
}
Now let's just say that you've got a really big tree somewhere in the hundreds of nodes and the
thousands of polygons. BSPs will be great for drawing everything in the right order, but isn't there
any way to save us from trying to draw a whole bunch of stuff that won't be seen anyhow? The answer
is yes, there are many. For now let's start with something basic, node boundings.
Bounding boxes and bounding spheres have been in use for ages. The simplest bounding is a sphere that
encompasses a certain amount of stuff. Four or Five really quick tests are all that you need to
determine if your camera can see the sphere and that tells you if you can see any of the stuff inside.
So how about a recursive function that walks through every node in the BSP tree and calculates the
smallest sphere needed to contain every part of the current node and it's leaves? That way the
instant you discover that a node is outside the camera view you can stop walking that branch because
you know that none of it's leaves are visible, either.
Some tips for debugging your BSP building algorithm:
- Limit the depth of recursion by using a static or global counter. increment it every time
you descend the tree and subtract when you go back. If the value gets to high, return immediately.
However, you have to be careful with this because the number of function calls is NOT linear with
the maximum value. what I mean is this: because every branch of the tree has two leaves it is very
possible that you have O(n2) calls to make. So if you pick a depth of 5 as your maximum
there will be 25 function calls. If you pick 10 you'll have a hundred function calls.
- Don't bite off more than you can chew. In other words, start with the simplest possible
model and work your way up. I recommend the following sets:
- two parallel polygons, each in front of the other.
- two parallel polygons, each behind the other.
- two polygons that are coplanar
- two square polygons that intersect each other
- two polygons that share one edge but are NOT coplanar.
If all those cases work, every case should work.
- If many polygons reference a single plane class be sure when splitting to use the polygon
normal or everything will be backwards and (especially in the case of leaf-based trees) all
hell will break loose.
So we've managed to cover how BSPs are built, how BSPs are rendered and a very quick way of clipping at
least some of the tree to save us CPU time. But there's more still to come! We're going to take a
look at Constructive Solid Geometry, Possible Visible Set and then get into some even cooler stuff like
mirrors and radiosity lighting. BSPs - the tree with a million uses.
Back to the top
PREV: Overall structure
NEXT: Constructive Solid Geometry
|