


Next: Equations
for Gating Variables Up: Hodgkin-Huxley-A
(HHA) Model
Voltage Equation
All parameters for the somatic compartment, with the exception of the adaptation
conductance and the coupling conductance between somatic and dendritic
compartments, are given by the standard model of Connor
et al. (1977). The evolution of the voltage in the somatic compartment
is given by the differential equation:
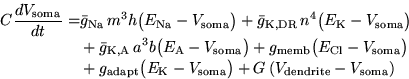 The peak conductances, measured per membrane area, are
The peak conductances, measured per membrane area, are
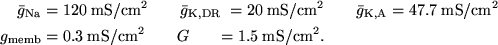
The variable adaptation conductance 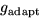 depends on the spiking frequency through a calcium accumulation mechanism,
which has been calibrated to yield a mean adaptation conductance of
depends on the spiking frequency through a calcium accumulation mechanism,
which has been calibrated to yield a mean adaptation conductance of 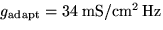 .(Further
details on the adaptation conductance in the Adaptation
subsection.)
.(Further
details on the adaptation conductance in the Adaptation
subsection.)
The reversal potentials are set to  mV,
mV, 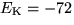 mV, and
mV, and 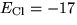 mV. Since the A-current is a potassium current, the associated reversal
potential should be
mV. Since the A-current is a potassium current, the associated reversal
potential should be 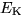 .
However, Connor
et al. (1977) redefined the reversal potential associated with
this conductance, setting it to
.
However, Connor
et al. (1977) redefined the reversal potential associated with
this conductance, setting it to  mV.
mV.
Martin Stemmler
1/14/1998
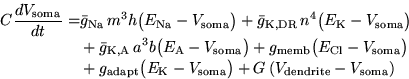
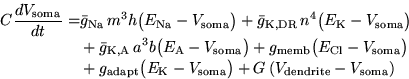
![]() mV,
mV, ![]() mV, and
mV, and ![]() mV. Since the A-current is a potassium current, the associated reversal
potential should be
mV. Since the A-current is a potassium current, the associated reversal
potential should be ![]() .
However, Connor
et al. (1977) redefined the reversal potential associated with
this conductance, setting it to
.
However, Connor
et al. (1977) redefined the reversal potential associated with
this conductance, setting it to ![]() mV.
mV.