 .
Given a generic point
p∈
.
Given a generic point
p∈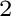 , we denote with d
the distance of p from the viewpoint v.
Our thershold function increases linearly with d
according to the expression
, we denote with d
the distance of p from the viewpoint v.
Our thershold function increases linearly with d
according to the expression
 (p) = cdistd,
where cdist is a positive constant.
(p) = cdistd,
where cdist is a positive constant.
Computing the viewshed of a given viewpoint v on a TIN T consists of determining the portions of each triangle of T that are visible from v.
The problem of viewshed computation has been extensively studied for TINs, and for general three-dimensional scenes. Viewsheds can be computed from an MT by extracting first a TIN at the desired resolution, and then applying one of the existing viewshed algorithm for TINs (see [#!DeFMag94!#] for a survey).
The most popular viewshed algorithms for TINs traverse the TIN triangles in front-to-back order with respect to the given viewpoint and compute the visible and invisible portions of each triangle directly during such traversal. They exploit the fact that a triangle σ can only be obscured by triangles that precede it in the front-to-back order; thus, when σ is traversed, we already have all necessary information to determine the visibility situations of σ.
Viewshed computation is an expensive task since the worst-case space complexity of the viewshed can be as high as Ω(n2) for a TIN with n vertices [#!ColSha89!#]. Thus, we can save time and computation resources by computing it on a terrain representation at a reduced resolution. In general, visibility computations are sensitive to elevation errors near the viewpoint; therefore it is recommended to ensure a sufficient accuracy near the viewpoint, and decrease it progressively with distance [#!FelGri90!#].
As in the case of interactive terrain visualization,
we define our threshold function in  .
Given a generic point
p∈
.
Given a generic point
p∈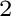 , we denote with d
the distance of p from the viewpoint v.
Our thershold function increases linearly with d
according to the expression
, we denote with d
the distance of p from the viewpoint v.
Our thershold function increases linearly with d
according to the expression
 (p) = cdistd,
where cdist is a positive constant.
(p) = cdistd,
where cdist is a positive constant.
A global query is performed in order to extract a TIN representing the whole terrain according to the variable-resolution criteria illustrated above. On such TIN, a viewshed algorithm is then applied. Since viewshed algorithms need adjacency information for the TIN on which they operate, such information is generated within the extraction algorithm.
The viewshed of a terrain is usually computed for either a fixed viewpoint, or for a fixed set of viewpoints (e.g. a set of facilities such as transmission or monitoring stations on a terrain). If the viewshed is computed just once, then the corresponding TIN can be extracted by applying a static query algorithm (which requires less memory).
In some situations, however, it might be useful to compute the
viewshed initially on a rather rough terrain representation, and then
refine it interactively in some interesting areas that are
determined based on the initial sketch of the distribution of visible
and invisible terrain areas.
In such cases it is necessary to modify the error threshold
function and extract a new TIN.
For instance, if the user decides to refine the viewshed
in a specific area A of the terrain, then the threshold function
must be redefined in such a way that it gives smaller values
(i.e., requires a more accurate representation),
for the view directions intersecting A.
Thus, the expression of the threshold function becomes
 (p) = cdist(θ)d,
where now cdist is a function of the angular position θ
of point p with respect to the viewpoint v
(see Figure
(p) = cdist(θ)d,
where now cdist is a function of the angular position θ
of point p with respect to the viewpoint v
(see Figure ![[*]](/file/20193/2015-02-11.ftp.disi.unige.it.tar/ftp.disi.unige.it/pub/.person/PuppoE/VARIANT/part2.tex/crossref.png) ),
and it can be changed interactively by the user.
),
and it can be changed interactively by the user.
 |
As cdist changes, a new TIN must be extracted and the corresponding viewshed must be computed. In such a context, it is interesting to use a dynamic TIN extraction combined with a dynamic viewshed algorithm. Dynamic viewshed algorithms maintain the visible portions of a set of triangles under on-line insertion and deletion of triangles [#!DeFMagCOSIT95!#,#!DobYvi93!#]. If we record the changes in the extracted TIN (i.e., the set of triangles that disappear and the ones that replace them), we can avoid recomputing the viewshed from scratch, and instead use a dynamic viewshed algorithm to update it by removing the contribution of the old triangles and inserting that of the new triangles.
TOLTO SU SUGGERIMENTO DI ENRICO
A dynamic viewshed algorithm intrinsecally
exhibits higher time complexity than a static one, and,
in particular, it cannot reach worst-case optimality.
In [#!DobYvi93!#,#!DeFMagCOSIT95!#],
the expected time complexity for updating the viewshed after
the insertion or deletion
of a triangle, when n triangles are present, is
O(n log n).
Now, we compare the cost of updating a viewshed against the
cost of recomputing it, in order to determine the extent to
which a dynamic approach is convenient.
Let n1 and n2 be the number of triangles in the
previous and in the current TIN, respectively.
Computing the new viewshed
by scratch takes a time equal, in the worst case, to
O((n2)2),
if the optimal algorithm by Edelesbrunner, Guibas and Sharir
[#!EdeGuiSha89!#] is used.
We denote by kold and knew, respectively, the number
of triangles appearing in the new TIN, and not in the old one,
and the number of triangles
appearing in the old TIN, and not in the new one.
(clearly,
kold≤n1 and
knew≤n2).
Updating the viewshed costs
O(koldn1log n1) for deletions,
and
O(knewn2log n2) for insertions.
We assume that the two TINs ``so close'' to each other
that n2 and
n2 = Θ(n).
The update of the viewshed is more efficient than its direct recomputation
if
O((kold + knew)n log n) is less than O(n2), i.e., if
kold, knew∈O(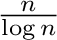 ).
).
A module for computing viewsheds from TINs extracted from a Multi-Triangulation is currently under implementation.