Visual and Vestibular Motion Detection

The visual-inertial nulling measure involves the interaction between visual and inertial motion cues. An important inertial motion detector for humans is the vestibular system in the inner ear. This section summarizes the relationship between visual and vestibular motion perception as it affects the visual-inertial nulling measure.

All of the nulling experiments described in this dissertation involved both visual and inertial sinusoidal oscillations in the horizontal plane at .1 Hz. The .1 Hz frequency was picked for two reasons. The first had to do with the dynamics of the semi-circular canals of the vestibular system, which detect angular accelerations of the head. As taken from Howard [46], natural head motions occur in the frequency range of .1 Hz to 5 Hz. The semi-circular canals are tuned for these frequencies. In this range, the detection of inertial oscillations should have a gain of close to 1 and very little phase offset. This implies that participants should be able to accurately detect the inertial oscillation in this frequency range (provided that the amplitude is sufficient). At higher frequencies, the canals exhibit phase lag; at lower frequencies, phase lead. To test the ability of visual cues to overwhelm inertial cues, we needed participants to be receiving accurate inertial information. This required that the experiment be conducted somewhere in the .1 Hz to 5 Hz range.

A second consideration was to pick a range in which both the visual and vestibular systems are used for motion detection. Otherwise, an effective conflict between the two could not be created. The visual system dominates at very low frequencies; the vestibular system, at high frequencies. The gain for the visual and inertial systems are equal at about .02 Hz [112]. This was a reason for picking the lowest value in the .1 Hz to 5 Hz range: it is closer to .02 Hz.

Aside from frequency considerations, the measurement of inertial amplitude is also an important issue. In principle, inertial amplitude can be measured in many ways, for instance: angular displacement; peak angular velocity; peak angular acceleration, etc. The best choice appears to be the maximum peak-to-peak difference in velocity across a complete cycle. This is because while the semicircular canals respond to accelerations in their individual planes of rotation, they integrate these accelerations to report velocities [46]. Benson et al. [9] mention that ``The frequency coded signals from the ampullary receptors [of the semicircular canals] are much more closely related to the angular velocity of the head than to its angular acceleration.'' They add that ``many experiments (reviewed by Guedry [31]) in which thresholds for the detection of whole-body rotation were determined have shown that threshold is primarily dependent upon the change of angular velocity ( ) achieved by the test stimulus rather than by its acceleration, provided the duration of the stimulus does not appreciably exceed the integration time constant of the semicircular canals.''

In the same paper, Benson et al. [9] give the mean threshold for the detection of whole body yaw rotations in 30 subjects as 1.5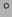/sec. The velocity stimulus followed a single cosine bell trajectory.