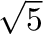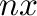×
containing samples of the function to be contoured. The parameters
kx, lx, ky and ly specify the portion of z
that is to be considered. The array clevel of length nlevel
is a list of the desired contour levels.
A routine is available in PLPLOT which performs a contour plot of data stored in a two-dimensional array. A contour following algorithm is used, so that it is possible to use non-continuous line styles.
The routine plcont has the form
plcont(z,nx,ny,kx,lx,ky,ly,clevel,nlevel,tr)
where z is the two-dimensional array of size
×
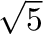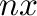containing samples of the function to be contoured. The parameters
kx, lx, ky and ly specify the portion of z
that is to be considered. The array clevel of length nlevel
is a list of the desired contour levels.
The path of each contour is initially computed in terms of the values of the
array indicies which range from 1 to nx in the first index and from
1 to ny in the second index. Before these can be drawn in the current
window (see page ![[*]](/file/6987/CAM_CD_1.iso/files/236.lha/PlPlot_v1.0/docs/chapter3.tex/crossref.png)
in Section ), it is necessary to
convert from these array indicies into world coordinates. This is done by
passing a pointer to a user-defined function to plcont. This
function pointer is the last argument tr.
This function must be declared as type void in the
module which calls plcont. This transformation function
must have the parameter list
void tr(x,y,tx,ty);
where (x,y)
is the point through which the contour runs expressed in
terms of array indicies, and (tx,ty) are pointers to float variables
which are the world coordinates of
the point which corresponds to these indicies.
Often, the transformation between array indicies and world coordinates can be expressed as a linear transformation. A routine is provided within the library which can be passed to plcont as the parameter tr. This transformation routine is as follows:
#include "plplot.h"
void xform(x,y,tx,ty)
float x, y, *tx, *ty;
{
extern float tr[];
*tx = tr[0]*x + tr[1]*y + tr[2];
*ty = tr[3]*x + tr[4]*y + tr[5];
}
Thus by setting up the values in the array tr[], we can
apply an arbitrary translation, rotation and/or shear to the array before
drawing out the contours. By defining other transformation subroutines,
it is possible to draw contours wrapped around polar grids etc.
As an example in setting up tr[], suppose that the array z is of size 21×41 and contains the values of the function z[x][y], where x ranges from 0.0 to 4.0 and y ranges from -8.0 to 8.0. Furthermore, let us also suppose that the window (as defined using plenv or plwind) covers this range of world coordinates. Since we wish the index (1,1) in array z to map to (0.0,-8.0) and the index (21,41) to map to (4.0,8.0), and for there to be no skew in the axes, we should choose elements of tr[] so that
| tx | = | |
| ty | = |