![[*]](crossref.png) .
.
In diesem Abschnitt werden die wichtigsten Elemente, die in mathematischen
Formeln verwendet werden, kurz beschrieben.
Eine Liste aller verf"ugbaren Symbole enth"alt Kapitel ![[*]](crossref.png) .
.
Kleine
griechische Buchstaben
werden als \alpha, \beta, \gamma, usw. eingegeben, gro"se griechische Buchstaben als
{\rm A}, {\rm B},
\Gamma, \Delta,
usw.
λ, ξ, π, μ, Φ, Ω
$\lambda, \xi, \pi, \mu, \Phi, \Omega $
Weiters gibt es eine F"ulle von mathematischen Symbolen:
von ∈ "uber
⇒ bis ∞
(siehe Kapitel ![[*]](crossref.png) ).
).
Exponenten und Indizes k"onnen mit den
Zeichen ^ und _ hoch- bzw. tiefgestellt werden.
a1
x2
e-αt
a3ij
$a_{1}$ \qquad
$x^{2}$ \qquad
$e^{-\alpha t}$ \qquad
$a^{3}_{ij}$
Das Wurzelzeichen wird mit \sqrt eingegeben,
n-te Wurzeln mit \sqrt[n].
Die Gr"o"se des Wurzelzeichens wird von LATEX automatisch gew"ahlt.


![$\sqrt[3]{{2}}$](img4.png)
$\sqrt{x}$ \qquad
$\sqrt{ x^{2}+\sqrt{y} }$
\qquad $\sqrt[3]{2}$
Die Befehle \overline und \underline bewirken
waagrechte Striche direkt "uber bzw. unter einem Ausdruck.

$\overline{m+n}$
Die Befehle \overbrace und \underbrace bewirken
waagrechte Klammern "uber bzw. unter einem Ausdruck.
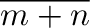
$\underbrace{ a+b+\cdots+z }_{26}$
Um mathematische "`Akzente"' wie Pfeile oder Schlangen auf
Variablen zu setzen, gibt es die
in Tab. ![[*]](crossref.png) angef"uhrten
Befehle.
L"angere Tilden und Dacherln, die sich "uber mehrere (bis zu 3)
Zeichen erstrecken k"onnen, erh"alt man mit
angef"uhrten
Befehle.
L"angere Tilden und Dacherln, die sich "uber mehrere (bis zu 3)
Zeichen erstrecken k"onnen, erh"alt man mit
\widetilde bzw. \widehat.
Ableitungszeichen werden mit ' (Apostroph) eingegeben.
\begin{displaymath}
y=x^{2} \qquad
y'=2x \qquad
y''=2
\end{displaymath}
Mathematische Funktionen werden in der Literatur "ublicherweise nicht kursiv (wie die Namen von Variablen), sondern in "`normaler"' Schrift dargestellt. Dazu gibt es die folgenden Befehle:
\arccos \cos \csc \exp \ker \limsup \min \sinh \arcsin \cosh \deg \gcd \lg \ln \Pr \sup \arctan \cot \det \hom \lim \log \sec \tan \arg \coth \dim \inf \liminf \max \sin \tanhF"ur die Modulo-Funktion gibt es zwei verschiedene Befehle:
\bmod f"ur den bin"aren Operator a mod b
und \pmod{...} f"ur die Angabe in der Form
x≡a(mod b).

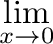 = 1
= 1
\begin{displaymath}
\lim_{x \to 0} \frac{\sin x}{x}
=1
\end{displaymath}
Ein Bruch (fraction)
wird mit dem Befehl \frac{...}{...} gesetzt.
F"ur einfache Br"uche kann man aber auch den Operator / verwenden.
1 Stunden
Stunden
 x
x x1/2
x1/2
$1\frac{1}{2}$~Stunden
\begin{displaymath}
\frac{ x^{2} }{ k+1 }\qquad
x^{ \frac{2}{k+1} }\qquad
x^{ 1/2 }
\end{displaymath}
Binomial-Koeffizienten k"onnen in der Form
{...\choose...} gesetzt werden.
Mit dem Befehl \atop erh"alt man das Gleiche ohne Klammern.


\begin{displaymath}
{ n \choose k } \qquad
{ x\atop y+2 }
\end{displaymath}
Das Integralzeichen wird mit \int eingegeben,
das Summenzeichen mit \sum.
Die obere und untere Grenze wird mit ^ bzw. _
wie beim Hoch/Tiefstellen angegeben.
Normalerweise werden die Grenzen neben das Integralzeichen
gesetzt (um Platz zu sparen), durch Einf"ugen des Befehl \limits
wird erreicht, da"s die Grenzen oberhalb und unterhalb des
Integralzeichens gesetzt werden.
Beim Summenzeichen hingegen werden die Grenzen bei
der Angabe von \nolimits oder im laufenden Text neben das
Summenzeichen gesetzt, ansonsten aber unter- und oberhalb.


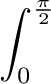
\begin{displaymath}
\sum_{i=1}^{n} \qquad
\int_{0}^{\frac{\pi}{2}} \qquad
\int \limits_{-\infty}^{+\infty}
\end{displaymath}
F"ur Klammern und andere Begrenzer gibt es in TEX viele verschiedene Symbole (z.B.
[ 〈 |  ).
Runde und eckige Klammern k"onnen mit den entsprechenden Tasten
eingegeben werden, geschwungene mit
).
Runde und eckige Klammern k"onnen mit den entsprechenden Tasten
eingegeben werden, geschwungene mit \{, die anderen mit
speziellen Befehlen (z.B. \updownarrow).
Setzt man den Befehl \left vor "offnende Klammern und
den Befehl \right vor schlie"sende, so wird automatisch die
richtige Gr"o"se gew"ahlt.


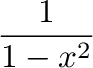
\begin{displaymath}
1 + \left( \frac{1}{ 1-x^{2} }
\right) ^3
\end{displaymath}
In manchen F"allen m"ochte man die Gr"o"se der Klammern lieber
selbst festlegen, dazu sind die Befehle
\bigl,
\Bigl,
\biggl und
\Biggl anstelle von \left
und analog \bigr etc. anstelle von \right anzugeben.
 (x + 1)(x - 1)
(x + 1)(x - 1)
\begin{displaymath}
\Bigl( (x+1) (x-1) \Bigr) ^{2}
\end{displaymath}
Um in Formeln 3 Punkte (z.B. f"ur 1,2,...,n) auszugeben,
gibt es die Befehle
\ldots und \cdots.
\ldots setzt die Punkte auf die Grundlinie (low),
\cdots setzt sie in die Mitte der Zeilenh"ohe (centered).
Au"serdem gibt es die Befehle
\vdots f"ur vertikale und
\ddots f"ur diagonale Punkte.
\begin{displaymath}
x_{1},\ldots,x_{n} \qquad
x_{1}+\cdots+x_{n}
\end{displaymath}