Primitives

Primitive objects are the building box with which other objects are created. Each primitive type has associated with it specialized methods for creation, intersection with a ray, bounding box calculation, surface normal calculation, ray enter/exit classification, and for the computation 2D texture coordinates termed u-v coordinates. This latter method is often referred to as the inverse mapping method.

While most of these methods should be of little concern to you, the inverse mapping methods will affect the way in which certain textures are applied to primitives. Inverse mapping is a matter of computing normalized u and v coordinates for a given point on the surface of the primitive. For planar objects, the u and v coordinates of a point are computed by linear interpolation based upon the u and v coordinates assigned to vertices or other known points on the primitive. For non-planar objects, uv computation can be considerably more involved.

This section briefly describes each primitive and the syntax that should be used to create an instance of the primitive. It also describes the inverse mapping method, if any, for each type.

$\begin{defprim}{blob}{{\em thresh st r} \evec{p} [{\em st r} \evec{p} \ldots]} ... ...by its position \evec{p}, radius {\em r}, and strength {\em st}. \end{defprim}$
The metaballs affect each other according to a superimposed density distribution:

F(x, y, z) = $\displaystyle \sum_{{i=0}}^{n}$ b_ie^-d_i - T = 0

There is no inverse mapping method for blobs.

$\begin{defprim}{box}{\evec{corner1} \evec{corner2}} Creates an axis-aligned box which has \evec{corner1} and \evec{corner2} as opposite corners. \end{defprim}$
Transformations may be applied to the box if a non-axis-aligned instance is required. There is no inverse mapping method for boxes.

$\begin{defprim}{sphere}{{\em radius} \evec{center}} Creates a sphere with the given {\em radius} and centered at the given position. \end{defprim}$
Note that ellipsoids may be created by applying the proper scaling to a sphere. Inverse mapping on the sphere is accomplished by computing the longitude and latitude of the point on the sphere, with the u value corresponding to longitude and v to latitude. On an untransformed sphere, the z axis defines the poles, and the x axis intersects the sphere at u = 0, v = 0.5. There are degeneracies at the poles: the south pole contains all points of latitude 0., the north all points of latitude 1.

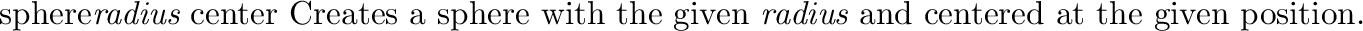
$\begin{defprim}{torus}{{\em rmajor rminor} \evec{center} \evec{up}} Creates a t... ...around the center point at a distance equal to the major radius. \end{defprim}$
In tori inverse mapping, the u value is computed using the angle of rotation about the up vector, and the v value is computing the angle of rotation around the tube, with v = 0 occuring on the innermost point of the tube.

$\begin{defprim}{triangle}{\evec{p1} \evec{p2} \evec{p3}} Creates a triangle with the given vertices. \end{defprim}$

$\begin{defprim}{triangle}{\evec{p1} \evec{n1} \evec{p2} \evec{n2} \evec{p3} \ev... ...Phong-shaded triangle with the given vertices and vertex normals. \end{defprim}$
For both Phong- and flat-shaded triangles, the u axis is the vector from p1 to p2, and the v axis the vector from p1 to p3. There is a degeneracy at p3, which contains all points with v = 1.0. This default mapping may be modified using the triangleuv primitive described below.

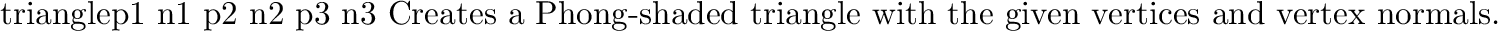
$\begin{defprim}{triangleuv}{\evec{p1} \evec{n1} \evec{uv1} \evec{p2} \evec{n2} ... ...uv} given for each vertex are used instead of the default values. \end{defprim}$
When computing uv coordinates within the interior of the triangle, linear interpolation of the coordinates associated with each triangle vertex is used.

$\begin{defprim}{poly}{\evec{p1} \evec{p2} \evec{p3} [\evec{p4} \ldots ]} Create... ...ber of vertices in a polygon is limited only by available memory. \end{defprim}$
Inverse mapping for arbitrary polygons is problematical. punts and equates u with the x coordinate of the point of intersection, and v with the y coordinate.

$\begin{defprim}{heightfield}{{\em file}} Creates a height field defined by the ... ...s rendered as a surface tessellated by right isosceles triangles. \end{defprim}$
See Appendix C for a discussion of the format of a height field file. Height field inverse mapping is straight-forward: u is the x coordinate of the point of intersection, v the y coordinate.

$\begin{defprim}{plane}{\evec{point} \evec{normal}} Creates a plane that passes through the given point and has the specified normal. \end{defprim}$
Inverse mapping on the plane is identical to polygonal inverse mapping.

$\begin{defprim}{cylinder}{{\em radius} \evec{bottom} \evec{top}} Creates a cyli... ...cated {\em radius}. Cylinders are rendered {\em without} endcaps. \end{defprim}$
The cylinder's axis defines the v axis. The u axis wraps around the cylinder, with u = 0 dependent upon the orientation of the cylinder.

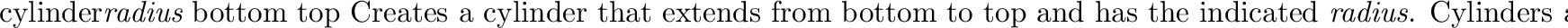
$\begin{defprim}{cone}{$rad_{bottom}$\ \evec{bottom} $rad_{top}$\ \evec{top}} Cr... ..._{top}$\ at \evec{top}. Cones are rendered {\em without} endcaps. \end{defprim}$
Cone inverse mapping is analogous to cylinder mapping.

$\begin{defprim}{disc}{{\em radius} \evec{pos} \evec{normal}} Creates a disc centered at the given position and with the indicated surface normal. \end{defprim}$
Discs are useful for placing endcaps on cylinders and cones. Inverse mapping for the disc is based on the computation of the normalized polar coordinates of the point of intersection. The normalized radius of the point of intersection is assigned to u, while the normalized angle from a reference vector is assigned to v.