Realizzazione di una rete neurale RBF.
(Dino Calvisi - Domenico Skworcow)
Addestramento della rete neurale RBF.
La rete neurale impiegata Φ una rete RBF (Radial Basis Function): la risposta della rete dipende dai pesi e dalla distanza del vettore d'ingresso dai diversi centri presenti nella rete.
La risposta al vettore d'ingresso X Φ :
 n2 = numero di centri della rete
n2 = numero di centri della rete
La funzione RBF scelta Φ la funzione gaussiana, con  :
:

L'errore commesso dalla rete sui dati del training set fornito Φ definito come segue :
 M = numero di elementi del Training Set
M = numero di elementi del Training Set
L'addestramento della rete viene eseguito utilizzando i dati del Training Set, minimizzando la funzione errore: al minimo dell'errore corrisponderα un comportamento "adeguato" della rete neurale. La ricerca del punto di
minimo sfrutta un metodo di ottimizzazione non lineare: si Φ utilizzato il metodo dell'antigradiente, impiegando il metodo di Armijo per la line search. La direzione di discesa viene quindi ottenuta semplicemente "negando"
le componenti del gradiente della funzione errore ed il passo  da utilizzare viene determinato secondo la condizione di Armijo.
da utilizzare viene determinato secondo la condizione di Armijo.
Per evitare che l'algoritmo convergesse verso punti stazionari non significativi, si Φ introdotta una perturbazione sull'errore: questo garantisce la compattezza degli insiemi di livello della funzione. Si definisce quindi:
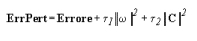
I valori dei parametri  vengono diminuiti ad ogni iterazione.
vengono diminuiti ad ogni iterazione.
L'algoritmo che risultante pu≥ essere cos∞ descritto:
Passo 0. Inizializzazione dei parametri della rete con valori casuali.
Inizializzazione dei pesi di perturbazione  .
.
I valori ottimali vengono inizializzati con i valori iniziali.
Passo 1. Si ricerca il minimo dell'errore perturbato col metodo dell'antigradiente.
Passo 2. Se i parametri ottenuti forniscono un errore non perturbato minore
dell'errore ottimale, si aggiornano i parametri ottimali con i parametri
correnti.
Passo 3. Se il criterio d'arresto Φ soddisfatto termina l'algoritmo,
altrimenti si decrementano  e si riprende dal passo 1
e si riprende dal passo 1
Il criterio d'arresto utilizzato Φ il seguente :
l'algoritmo termina se una delle seguenti condizioni Φ verificata
-  sono entrambi nulli (minori di una tolleranza fissata);
sono entrambi nulli (minori di una tolleranza fissata);
- l'errore Φ minore del valore atteso;
A tale schema si Φ apportata in realtα una piccola modifica: il problema non perturbato viene risolto per primo, successivamente
si passa a risolvere i problemi perturbati. Questo consente di ottenere subito la soluzione corretta se il problema iniziale non Φ affetto da problemi di saturazione. In caso contrario si andranno a risolvere i problemi perturbati.
Ottimizzazione: antigradiente e metodo di Armijo.
Per la minimizzazione della funzione obiettivo si utilizza la "direzione di discesa" fornita dall'antigradiente e il "passo" fornito dal metodo di Armijo. Questo richiede ovviamente la conoscenza delle componenti del gradiente della funzione errore.
Le varie componenti sono ottenibili come somma delle componenti riferite ad ogni punto del training set :

Per il calcolo di queste si Φ utilizzata la formula di derivazione a catena, ovvero :
ponendo:
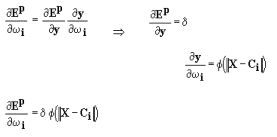

In questo modo Φ possibile ottenere facilmente le componenti del gradiente dell'errore. Il calcolo del gradiente dell'errore perturbato richiede solamente l'introduzione dei termini in  . Il gradiente diviene quindi :
. Il gradiente diviene quindi :

Per determinare il passo si utilizza la condifzione di Armijo. L'algoritmo di ottimizzazione Φ dunque il seguente :
Passo 0. Inizializzazione dei valori iniziali.
Passo 1. Se si verifica la condizione fine delle iterazioni, altrimenti si procede con il Passo 2.
fine delle iterazioni, altrimenti si procede con il Passo 2.
Passo 2. Si calcola la direzione di discesa :
Utilizzando il metodo di Armijo si determina il passo 
FinchΦ si verifica :
si pone :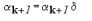
Si pone ora :
Passo 3. Si ritorna al Passo 1.
Soluzione del problema assegnato.
Il problema assegnato richiede la realizzazione di una rete neurale in grado di classificare i punti su di una scacchiera di 9 caselle. Il training set a disposizione Φ costituito da 45 elementi cos∞ disposti nel piano :

I punti sono cos∞ classificati : X => -1
O => +1
Per valutare la bontα dei parametri della rete ottenuti dall'addestramento si sono utilizzati dei dati di test, riportati di seguito :


I punti sono cos∞ classificati : X => -1
O => +1
Dimensioni della rete RBF.
Per la costruzione della rete adatta al riconoscimento della scacchiera descritta dal training set saranno necessari n2 centri: il numero di centri da utilizzare non Φ determinabile a priori. Lo scopo che ci si prefigge Φ ottenere un algoritmo sufficientemente veloce, che non impieghi quindi risorse di calcolo eccessive, e possibilmente che fornisca dei risultati sufficientemente precisi. La ricerca di un punto "ottimo" per l'errore della rete non deve far dimenticare lo scopo di una rete neurale: la rete che si ottiene deve essere in grado di fornire risposte "coerenti" proprio per valori di ingresso non appartenenti al training set. La ricerca di un errore molto piccolo sui dati del training set, od addirittura di un errore nullo, potrebbe risultare controproducente: si rischia di ottenere una rete che risponde perfettamente agli ingressi che giα si sanno classificare, ma che potrebbe fornire risposte completamente errate per ingressi diversi da questi. Si deve cercare un compromesso tra la semplicitα della rete e l'errore commesso sul training set.
Il modello di rete neurale descritto fin qui Φ stato sottoposto a diversi addestramenti variando il numero n2 di centri della rete; per ogni differente rete RBF sono riportati di seguito:
╖ errore commesso sul training set (ERR.TS);
╖ errore commesso sui dati di test (ERR.TEST);
╖ tempo medio necessario per un'iterazione del metodo dell'antigradiente (TMPI);
╖ numero di iterazioni del metodo dell'antigradiente necessarie per risolvere il
problema non perturbato (NIR);
╖ disposizione dei centri della rete nel piano;
Rete con 9 centri.
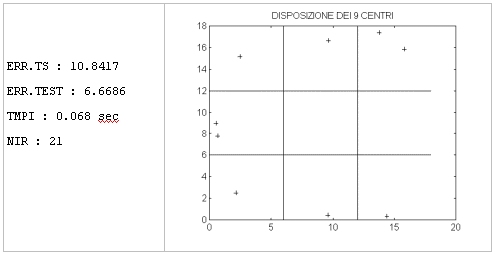
Rete con 20 centri.

Rete con 45 centri

Rete con 80 centri.
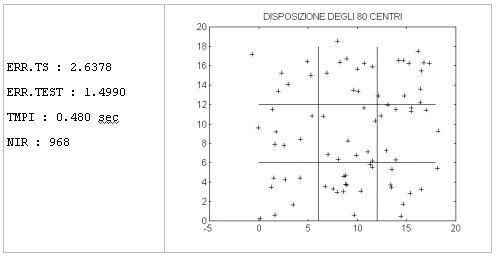
Rete con 100 centri

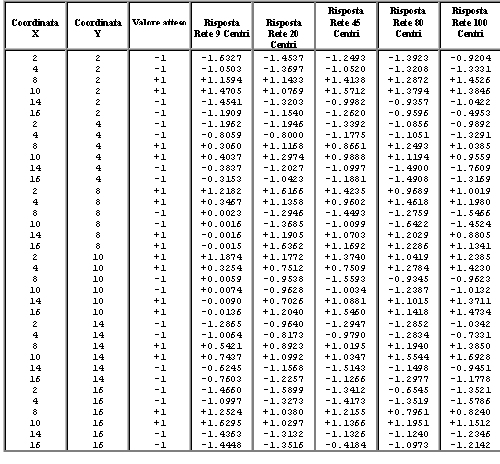
I valori dei parametri ottenuti al termine dell'addestramento di ogni rete sono riportati nell'Appendice A.
I tempi riportati sono stati rilevati utilizzando un'implementazione dell'algoritmo descritto: l'algoritmo Φ stato implementato utilizzando il linguaggio C++ (Borland Turbo C 3.0), senza tenere particolarmente conto di eventuali accorgimenti atti a ridurre i tempi di elaborazione; tale implementazione non ottimizzata dell'algoritmo Φ per≥ stata utilizzata per tutti i rilevamenti, che possono perci≥ dare un'idea del costo computazionale relativo all'addestramento di ciascuna rete.
Il listato dell'algoritmo viene riportato in Appendice B .
Si pu≥ ora analizzare la risposta che ogni rete fornisce ai dati di test scelti :
L'errore commesso sui dati del training set, diminuisce aumentando il numero dei centri (risale leggermente passando da 80 a 100 centri a causa dei limiti dell'implementazione dell'algoritmo).

Osservando il grafico si nota come la rete con 20 centri sia pi∙ efficace nel riconoscimento dei dati di test scelti: si tratta di dati disposti ben all'interno delle caselle che compongono la scacchiera. Tenendo inoltre conto del tempo di elaborazione richiesto per l'addestramento, la rete con 20 centri sembrerebbe la scelta migliore.
Si pu≥ ora controllare la risposta fornita dalla rete per alcuni punti vicini al confine tra due caselle diverse. Vengono prese in considerazione la rete con 20 centri (modello che ha fornito l'errore pi∙ basso sui dati ti test) e la rete con 80 centri (modello che ha fornito l'errore sul training set pi∙ basso). I nuovi dati di test sono distribuiti come rappresentato nel seguente grafico :
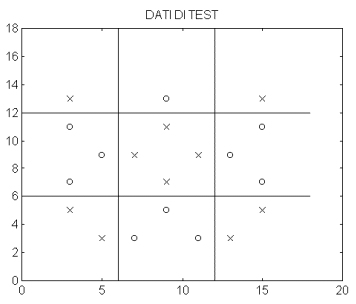
I punti sono cos∞ classificati : X => -1
O => +1

Riassumendo il comportamento complessivo della rete neurale con 20 e con 80 centri:

Nonostante l'errore commesso sui dati del training set sia maggiore, la rete con 20 centri commette errore minore sui dati di test utilizzati: non Φ detto infatti che diminuendo l'errore sul training set si debba necessariamente ottenere una rete migliore.
Iterazioni dell'algoritmo di addestramento relative alla rete
con 20 centri.
L'algoritmo di addestramento relativo alla rete a 20 centri, con perturbazioni = = 0.000025 ha prodotto le seguenti iterazioni (per ogni iterazione si riportano i valori dell'errore, dell'errore perturbato e il quadrato della norma del gradiente dell'errore perturbato):


Il grafico si riferisce al quadrato della norma dell'errore perturbato. Non vengono riportate le iterazioni precedenti alla 20a iterazione per rendere pi∙ leggibile il grafico stesso.
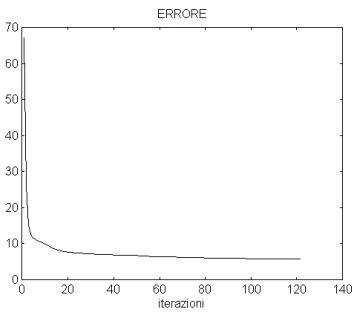
Il grafico riporta l'andamento dell'errore non perturbato: come si nota l'errore diminuisce ad ogni iterazione, fornendo una funzione monotona decrescente.
L'errore perturbato differisce molto poco dall'errore non perturbato (come si nota dai valori riportati nella tabella precedente), per tale motivo non ne viene proposto il grafico dell'andamento.
Appendice A.
Parametri della rete RBF dopo l'addestramento.



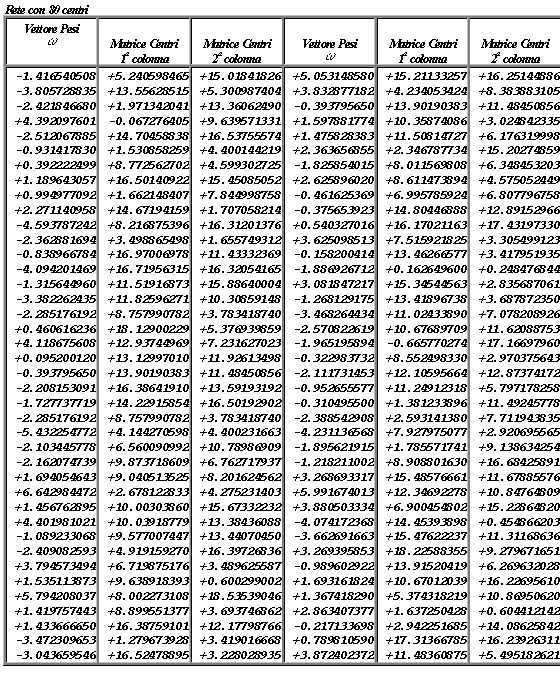

Appendice B.
Di seguito vengono proposti i listati dei file che compongono il programma relativo all'implementazione in linguaggio C++ della rete neurale RBF descritta, inseriti nel file seguente:
Download dei listati