Como hicimos el mes pasado, vamos a introducir un nuevo objeto a nuestro raytracing. En esta ocasión le toca al turno a los cilindros (infinitos), otro de los objetos clásicos del raytracing, utilizando para ello un desarrollo similar. Primero, estudiaremos un caso concreto, los cilindros orientados paralelamente a los ejes, y después lo generalizaremos para conseguir cilindros orientados en cualquier dirección y, como novedad, elipsoides.
|
EL CILINDRO ES OTRO DE LOS OBJETOS CLÁSICOS DEL RAYTRACING. ES RELATIVAMENTE FÁCIL DE CALCULAR Y PERMITE HACER ESCENAS MÁS COMPLEJAS.
|
 Cilindros paralelos a los ejes Cilindros paralelos a los ejes
Para empezar invocaremos la ecuación del cilindro. Como en el caso de los planos, hay tres casos concretos de cilindro que son más fáciles de tratar, pero en este caso, son los cilindros paralelos a los ejes canónicos o globales (ver Figura 1). Sus ecuaciones son:
(Y-b)^2+(Z-c)^2=Radio^2 (cilindro paralelo al eje X)
(X-a)^2+(Z-c)^2=Radio^2 (cilindro paralelo al eje Y)
(X-a)^2+(Y-b)^2=Radio^2 (cilindro paralelo al eje Z)
Recordemos que ^2 equivale "elevado al cuadrado", "Radio" el radio del cilindro y los valores (a,b,c) indican la posición del cilindro (ver Figura 2). Lo primero que salta a la vista es que estas ecuaciones son muy parecidas a las de la esfera, con la salvedad de que en cada una de ellas ha "desaparecido" una de las componentes del espacio:
(X-a)^2+(Y-b)^2+(Z-c)^2=R^2 (esfera centrada en el punto (a,b,c))
|
COMO EN EL CASO DE LOS PLANOS, LOS CILINDROS ORIENTADOS EN LA DIRECCIÓN DE LOS EJES CANÓNICOS SON MÁS FÁCILES DE CALCULAR
|
Como veremos más adelante, esto tendrá implicaciones interesantes. A continuación nos centraremos en una sola de estas ecuaciones, la del cilindro orientado en la dirección del eje Z. Si recuperamos la ecuación del rayo y la introducimos dentro de la del cilindro
(X,Y,Z)=(Xo,Yo,Zo)+t*(Xi,Yi,Zi) (ecuación del rayo o la recta)
veremos que obtenemos de nuevo una ecuación de segundo grado cuya incógnita es ‘t’:
(Xo+t*Xi-a)^2+(Yo+t*Yi-b)^2=R^2
(Xi^2+Yi^2)*t^2+(Xi*(Xo-a)+ Yi*(Yo-b))*2t+(Xo-a)^2+ (Yo-b)^2-R^2=0
Esta ecuación vuelve a ser muy parecida a la que nos encontramos con la esfera pero, de nuevo, faltan las componentes "Z". Esto es un inconveniente, ya que en el caso de la esfera se podía simplificar el término (Xi^2+Yi^2+Zi^2) ya que suponíamos que la dirección del rayo estaba normalizada, por lo que su módulo al cuadrado (y este término es precisamente eso) valía 1. Con los cilindros, este término no se puede simplificar tan fácilmente. Como hicimos la otra vez, podemos resolver esta ecuación con la regla que se enseña a todo el mundo en la escuela:
A*X^2+B*X+C=0
X=(-B+raíz(B^2-4*A*C))/2A
|
PARA DEFINIR LA ORIENTACIÓN DE LOS CILINDROS UTILIZAREMOS EL EJE Z DE SU SISTEMA DE EJES. DE MOMENTO, LOS EJES X E Y LOS DEJAREMOS SIN UTILIZAR
|
Donde raíz(X) es la raíz cuadrada de X. En este caso, sólo tenemos que igualar:
A = (Xi,Yi,0)·(Xi,Yi,0) = (Xi^2+Yi^2)
B = 2*((Xi,Yi,0)·(Xo-a,Yo-b,0)) = ((Xi*(Xo-a)+Yi*(Yo-b))*2
C = (Xo-a,Yo-b,0)·(Xo-a,Yo-b,0)-R^2 = (Xo-a)^2+(Yo-b)^2-R^2
Y entonces encontrar el valor de ‘t’ es fácil y, con este valor, también resulta muy sencillo encontrar la posición (X,Y,Z) del punto de intersección a partir de la ecuación del rayo. Aún nos falta un pequeño detalle, y este es el vector normal (Nx,Ny,Nz) en ese punto de intersección, que necesitaremos tanto para la iluminación como para los reflejos. En este caso, un poco de geometría (ver Figura 3) nos da directamente que la normal es:
-x=(X-a)/R
-y=(Y-b)/R
-z=0
Otra vez salta a la vista que es exactamente lo mismo que en el caso de la esfera, pero sin tener en cuenta la coordenada Z.
 Consideraciones sobre los cilindros Consideraciones sobre los cilindros
Acabamos de ver cómo calcular un cilindro paralelo al eje Z, pero se puede seguir el mismo método para cilindros paralelos a los ejes X e Y del sistema global de ejes. En todos los casos, como hemos ido viendo en el del eje Z, nos encontraremos que las ecuaciones que aparecen son las mismas que en el caso de la esfera, pero se puede comprobar que siempre se "ignora" una de las coordenadas. Pensando un poco sobre el tema, uno se da cuenta que lo que hacemos es simplemente resolver el problema de la intersección en dos dimensiones, ignorando la tercera. Es decir, es como si se estuviese haciendo raytracing sobre un plano (en vez del espacio) y se calculase la intersección de los rayos con el equivalente plano de la esfera: el círculo. El hecho de hacer desaparecer una de las dimensiones en los cálculos se traduce de forma sencilla en que el objeto original (la esfera) se estira infinitamente, en las tres dimensiones, en la dirección de la coordenada que eliminamos (ver Figura 4).
Lo que nosotros hemos descrito cómo "eliminar" la coordenada Z de un vector tiene una traducción al lenguaje matemático un poco más compleja, y es "restar a un vector su proyección sobre el eje Z", o lo que es equivalente, "proyectar sobre el plano X-Y". Veamos cómo funciona esto. Habíamos comentado ya que "proyectar" sobre un eje es realizar la operación:
((X,Y,Z)·Eje)*Eje
Donde U·V es el producto escalar entre dos vectores, k*V el producto de un vector por un número y "Eje" el eje sobre el que proyectamos. Veamos cómo realmente podemos expresar el proceso de eliminar la coordenada Z a partir de esto:
(X,Y,Z)-((X,Y,Z)·Eje_Z)*Eje_Z =
(X,Y,Z)-((X,Y,Z)·(0,0,1))*(0,0,1) =
(X,Y,Z)-(Z)*(0,0,1) = (X,Y,Z)-(0,0,Z) =
(X,Y,0)
La idea es que en lugar de utilizar un procedimiento específico para calcular cilindros, se puede proyectar sobre un plano y después utilizar el mismo procedimiento que con las esferas.
 Cilindros en cualquier dirección Cilindros en cualquier dirección
Para conseguir un cilindro orientado en una dirección cualquiera simplemente utilizaremos un vector "orientación" arbitrario, que utilizaremos para proyectar sobre un plano y seguir con los cálculos normales para la esfera. Como hicimos con el plano, definiremos un conjunto de tres ejes perpendiculares y unitarios para cada cilindro y utilizaremos el EjeZ de este nuevo sistema de ejes (que no tiene por qué ser el (0,0,1)) para realizar los cálculos. El procedimiento para calcular la intersección de un rayo de luz con un cilindro será parecido a éste:
El primer paso es proyectar el vector dirección del rayo de luz utilizando el EjeZ (orientación)
D=(Xi,Yi,Zi)-((Xi,Yi,Zi)·EjeZ)*EjeZ
Si resulta que el vector dirección proyectado "D" es (0,0,0) entonces es que el rayo era paralelo al cilindro y no hay intersección posible (ver Figura 5), con lo que nos podemos evitar los demás cálculos:
|
EL PUNTO (a,b,c) INDICA LA POSICIÓN POR LA QUE PASARÍA EL CENTRO DEL CILINDRO. ADEMÁS, SI CAMBIAMOS LA ORIENTACIÓN DEL CILINDRO, ÉSTE ROTARÍA ALREDEDOR DE ESTE PUNTO
|
Después restamos al origen del rayo la posición del objeto (a,b,c) obteniendo un nuevo vector P’
P’=(Xo,Yo,Zo)-(a,b,c)
Que también proyectaremos utilizando el EjeZ del objeto, obteniendo el vector P:
P=P’-(P’·EjeZ)*EjeZ
Y con estos vectores, resolveremos la ecuación de segundo grado sobre ‘t’ que nos salía al calcular la esfera:
A*t^2+B*t+C=0
Con:
A=D·D
B=2*(P·D)
C=P·P-Radio^2
Para calcular el vector normal a la superficie en un punto (X,Y,Z), tenemos que volver a proyectar:
V’= (X,Y,Z)-(a,b,c)
V=V’-(V’·EjeZ)*EjeZ
N=V*(1/Radio)
Donde N es el vector normal que estábamos buscando. Y con esto, y las ‘t’ (recordemos que una ecuación de segundo grado puede tener dos soluciones) ya tenemos todo lo necesario para dibujar cilindros.
 Elipsoides Elipsoides
Si estiramos una esfera un poco, sin llegar al infinito (como en el caso del cilindro) conseguiremos otra figura geométrica llamada elipsoide (el equivalente tridimensional a una elipse). Esto puede conseguirse añadiendo un factor de escalado al proceso de proyectar los vectores:
V=V’-k*(V’·EjeZ)*EjeZ
Dependiendo del valor de ‘k’ conseguiremos un efecto u otro:
k=0 : Esfera convencional
0<k<1 : Esfera "alargada" en la dirección del EjeZ
k=1 : Cilindro
|
A PARTIR DE LOS CILINDROS SE PUEDEN CONSEGUIR ELIPSOIDES (ESFERAS ALARGADAS). UNA ESCENA EN LA QUE SE MUESTRE LA METAMORFOSIS DE ESFERAS EN CILINDROS PUEDE SER BASTANTE ESPECTACULAR
|
Otros valores de ‘k’ permiten obtener esferas "achatadas" y otros curiosos efectos colaterales (sobretodo con valores muy grande) pero aparecen problemas con el signo de la normal y con la precisión. Una forma fácil de implementar esto es utilizando un EjeZ que no esté normalizado, pero esto se contradice con la forma como habíamos definido el sistema de ejes. El decidirse sobre cómo introducir esto es ya cuestión de las preferencias de uno, sobretodo según lo complejo que pueda llegar a ser el raytracing que se hace.
Pues bien, ahora ya tenemos esferas, elipses, cilindros y planos. Con estos objetos ya se puede empezar a crear escenas un tanto complejas y vistosas, pero siempre hay que ir con cuidado con la velocidad.
|
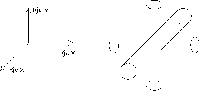 |
| En este esquema se pueden ver tres cilindros paralelos a los ejes X,Y y Z. Aunque no pasen por el origen de coordenadas, estos casos concretos son los más fáciles de calcular. |
|
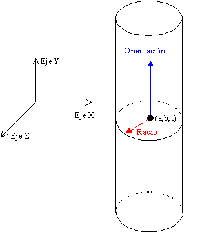 |
| En este caso tenemos un cilindro orientado en la dirección del eje Y ya que su eje de simetría (una recta imaginaria que pasa por el medio del cilindro) es paralelo al eje Y. Tal y como se ha definido, el punto (a,b,c) forma parte de esta recta imaginaria y permite desplazar el cilindro del origen de coordenadas, mientras que el radio indica la anchura del cilindro. |
|
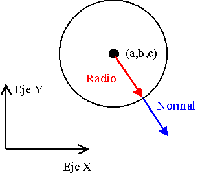 |
| Como se puede ver en esta imagen que representa un cilindro visto desde "arriba", el vector normal a la superficie de un punto en el cilindro es paralelo al vector que va desde el "centro" del cilindro a dicho punto, cuya norma sabemos que es el radio del cilindro. |
|
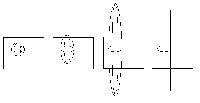 |
| Si estiramos una esfera hasta el infinito, al final obtendremos un cilindro (también infinito). Se puede ver en la definición del cilindro que sólo aparecen dos coordenadas del espacio, por lo que en realidad trata de un problema bidimensional. |
|
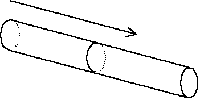 |
| Cuando un rayo de luz (una recta) es paralelo a un cilindro, entonces nunca se produce una intersección entre el rayo y el cilindro, de forma parecida a lo que sucedía cuando un rayo de luz era paralelo a un plano. Aunque no sean paralelos, sólo sabremos si hay intersección hasta que no empecemos a resolver la ecuación de segundo grado. |
|
 |
| Esta secuencia de imágenes muestra tres esferas superpuestas que se estiran en las direcciones de los ejes (pasando a ser elipsoides) hasta convertirse en cilindros. El cilindro violeta es paralelo al eje X, el cían al eje Y, y el amarillo al eje Z. |
|
 |
| Esta imagen tomada de la Platipus de Incognita muestra una escena generada por raytracing formada básicamente por cilindros. Incluso las "paredes" de la habitación son un cilindro visto desde el interior. Como se puede apreciar, la utilización de texturas hace la escena aún más vistosa. |
|
|





