
Obr. 1: Frustum
Středem pozornosti v dnešní nové lekci bude třída CTerrain a XCamera. S druhou jmenovanou třídou jsme již pracovali v minulé a předminulé lekci, dnes ji tedy pouze doplníme, abychom mohli ořezávat viditelnou scénu. Naopak třídu CTerrain budeme vytvářet úplně od začátku.
O Frustum jsme si pověděli, že je to komolý jehlan, který vymezuje prostor. Všechny objekty, které jsou uvnitř tohoto prostoru, by se měly vykreslit, protože budou vidět. U ostatních objektů je jistota, že vidět nebudou a tím pádem nás nezajímají. Důležité je tedy zajistit, abychom vykreslovali jen ty objekty, které uvnitř jsou a zbytečně neplýtvali výkon těmi ostatními. Abychom takový test mohli vůbec provést, je třeba mít Frustum spočítané a to je úkol této části.
Opět budeme používat hojně pojmů z analytické geometrie. Základ je struktura CLIPVOLUME, která pomocí obecných rovnic rovin přesně definuje Frustum:
typedef struct _CLIPVOLUME
{
D3DXPLANE pLeft, pRight;
D3DXPLANE pTop, pBottom;
D3DXPLANE pNear, pFar;
} CLIPVOLUME;
D3DXPLANE určuje čtyřmi koeficienty a, b, c a d rovnici roviny ve tvaru:
ax + by + cz + d = 0
Což je obecná rovnice roviny v prostoru. Koeficienty a, b a c tedy určují normálový vektor roviny. Atributy pLeft a pRight určují boky, pTop a pBottom je strop a podlaha a nakonec pNear a pFar jsou přední a zadní stěna.

Obr. 1: Frustum
Úkolem je tedy určit všech šest rovin co nejpřesněji. Vypadá to jako nepřekonatelný problém, ale ve skutečnosti je to trochu analytické geometrie ze střední školy. Následuje nová metoda třídy XCamera, která určí Frustum naší kamery:
void XCamera::ComputeClipVolume()
{
FLOAT dist, t1, t2;
D3DXVECTOR3 p, pt[8];
D3DXVECTOR3 v1, v2, n;
D3DXVECTOR3 vUpDir = D3DXVECTOR3(0.0f, 0.0f, 1.0f);
D3DXVECTOR3 vDir = m_vLookAtPoint - m_vEyePt ;
D3DXVECTOR3 vCross;
D3DXVec3Cross(&vCross, &vUpDir, &vDir);
D3DXVec3Cross(&vUpDir, &vDir, &vCross);
D3DXVec3Normalize(&vDir, &vDir);
D3DXVec3Normalize(&vCross, &vCross);
D3DXVec3Normalize(&vUpDir, &vUpDir);
for(INT i = 0; i < 8; i++)
{
dist = (i & 0x4) ? FAR_CLIP : NEAR_CLIP;
pt[i] = dist * vDir;
t1 = dist * tanf(FOV/2);
t1 = (i & 0x2) ? t1 : -t1;
pt[i] += vUpDir * t1;
t2 = dist * tanf(FOV/2) * ASPECT; // take into account screen proportions
t2 = (i & 0x1) ? -t2 : t2;
pt[i] += vCross * t2;
pt[i] += m_vEyePt;
}//compute the near plane
v1 = pt[2] - pt[0];
v2 = pt[1] - pt[0];
D3DXVec3Cross(&n, &v2, &v1);
D3DXVec3Normalize(&n, &n);
m_CV.pNear.a = n.x;
m_CV.pNear.b = n.y;
m_CV.pNear.c = n.z;
m_CV.pNear.d = -(n.x * pt[0].x + n.y * pt[0].y + n.z * pt[0].z);//compute the far plane
v1 = pt[5] - pt[4];
v2 = pt[6] - pt[4];
D3DXVec3Cross(&n, &v2, &v1);
D3DXVec3Normalize(&n, &n);
m_CV.pFar.a = n.x;
m_CV.pFar.b = n.y;
m_CV.pFar.c = n.z;
m_CV.pFar.d = -(n.x * pt[4].x + n.y * pt[4].y + n.z * pt[4].z);// - 10.0f;//compute the top plane
v1 = pt[6] - pt[2];
v2 = pt[3] - pt[2];
D3DXVec3Cross(&n, &v2, &v1);
D3DXVec3Normalize(&n, &n);
m_CV.pTop.a = n.x;
m_CV.pTop.b = n.y;
m_CV.pTop.c = n.z;
m_CV.pTop.d = -(n.x * pt[2].x + n.y * pt[2].y + n.z * pt[2].z);//compute the bottom plane
v1 = pt[1] - pt[0];
v2 = pt[4] - pt[0];
D3DXVec3Cross(&n, &v2, &v1);
D3DXVec3Normalize(&n, &n);
m_CV.pBottom.a = n.x;
m_CV.pBottom.b = n.y;
m_CV.pBottom.c = n.z;
m_CV.pBottom.d = -(n.x * pt[0].x + n.y * pt[0].y + n.z * pt[0].z);//compute the left plane
v1 = pt[3] - pt[1];
v2 = pt[5] - pt[1];
D3DXVec3Cross(&n, &v2, &v1);
D3DXVec3Normalize(&n, &n);
m_CV.pLeft.a = n.x;
m_CV.pLeft.b = n.y;
m_CV.pLeft.c = n.z;
m_CV.pLeft.d = -(n.x * pt[1].x + n.y * pt[1].y + n.z * pt[1].z);//compute the right plane
v1 = pt[4] - pt[0];
v2 = pt[2] - pt[0];
D3DXVec3Cross(&n, &v2, &v1);
D3DXVec3Normalize(&n, &n);
m_CV.pRight.a = n.x;
m_CV.pRight.b = n.y;
m_CV.pRight.c = n.z;
m_CV.pRight.d = -(n.x * pt[0].x + n.y * pt[0].y + n.z * pt[0].z);
}
Vypadá to možná děsivě, ale nyní si vše podrobně vysvětlíme. Pomohou nám následující obrázky. V horní části je vidět vztah mezi třemi důležitými vektory: vDir, vUpDir a vCross. To se také týká první části v kódu, kde od sebe odečteme LookAtPoint a EyePoint a tím získáme vektor kamery vDir. Dále potřebujeme vektor vCross, který je kolmý k vDir, ale zároveň musí být kolmý k vektoru vUpDir. Použijeme tedy vektorový součin. Potíž je v tom, že vUpDir nemusí mířit přímo nahoru, ale bude nakloněn tak, aby byl kolmý na vDir, který bude v našem případě mířit spíš k terénu. Musíme tedy zpětně využít vektor vCross a spočítat správný svislý vektor (opět pomocí vektorového součinu). Nakonec všechny tyto vektory znormalizujeme, aby měly jednotkovou velikost.
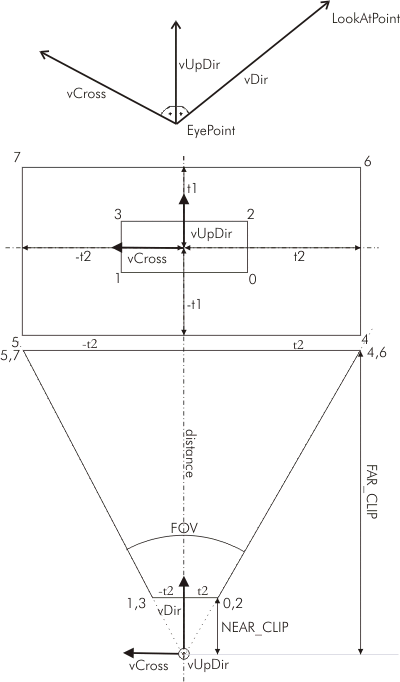
Obr. 2: Frustum v detailu
Na dalších obrázcích je vidět Frustum směrem od kamery a shora. FOV je úhel pohledu, který máme definovaný jako PI/4, tedy 45 stupňů. V cyklu inicializujeme osm bodů komolého jehlanu (čísla bodů jsou vyznačena na obrázku: 0-7). Nejprve počítáme přední stěnu, poté zadní, použijeme tedy buď konstantu NEAR_CLIP nebo FAR_CLIP. Poté protáhneme vektor vDir o vzdálenost stěny od kamery, tím se dostaneme do středu dané stěny. Proměnné t1 a t2 představují posun ve vertikálním resp. horizontálním směru. Spočítáme je úplně jednoduše pomocí tangenty úhlu FOV/2 (protilehlá ku přilehlé, protilehlá je zde požadovaná proměnná t1/t2 a přilehlá je vzdálenost od kamery - tedy buď NEAR_CLIP nebo FAR_CLIP. Proč bereme jen polovinu uhlu FOV je vidět s obrázku. U t2 navíc musíme počítat s tím, že Frustum nemá čtvercovou podstavu, ale že hrany jsou v poměru 4:3 (konstanta ASPECT). Podle bodu, který zrovna počítáme bude t1/t2 buď kladné nebo záporné a posuneme bod ve směru vDirUp a vCross. Na závěr jen posuneme Frustum do skutečné pozice kamery.
Nyní už bude hračka určit stěny Frustum, neboť máme hned čtyři body, které leží v každé rovině (dokonce by stačily tři). Již jsem zmínil, že koeficienty a, b, c obecné rovnice roviny w, jsou složky normálového vektoru n. Určíme tedy normálové vektory. To provedeme zcela jednoduše. Vybereme si libovolné tři body u každé stěny a spočítáme z nich dva směrové vektory s1 a s2, které leží v rovině w. Poté použijeme vektorový součin k určení vektoru kolmého na oba směrové vektory s1 a s2. To jsme ale získali vektor kolmý na rovinu w, protože s1 a s2 ležely v rovině w a získali jsme tudíž požadovaný vektor n. Zbývá umístit rovinu v prostoru, tedy určit koeficient d. Ten získáme zpětným dosazením libovolného bodu, který leží v rovině, do stávající rovnice. Po úpravách předchozí rovnice dostaneme:
d = -(ax + by + cz)
a, b a c již máme. x, y a z určují bod v rovině (můžeme si vybrat libovolný z těch čtyř, které známe). Tyto výpočty provedeme pro každou stěnu Frustum zvlášť.
V další části se budeme zabývat třídou CTerrain, která zapouzdří to, co jsme dělali v minulé lekci, to znamená tvorbu terénu a navíc k tomu přidáme podporu optimalizace pomocí quad tree. O stromech se dozvíte více v příští lekci Kurzu o datových strukturách. Nám ale budou stačit úplné základy. Navíc teorii jsme již probrali minule a implementace není příliš složitá (pokud znáte rekurzi).
Začneme tedy postupně. Základ bude struktura QTNode, která reprezentuje jeden uzel, popřípadě list stromu.
struct QTNode {
//
// Type of node - NODE, LEAF
NODETYPE ntType;
//
// Bounding points
BoundingPoint arBounds[4];
//
// Each node has four branches/children/kids
// LEAF has not any kids
QTNode *pBranches[4];
//
// leaf's tiles, each LEAF has 25 vertices (2 triangles per tile -> 32 triangles per LEAF)
// NODE has not any vertices
IVertexBuffer *pVB;
BOOL bVis;
};
Struktura obsahuje typ uzlu (buď se jedná o obyčejný uzel nebo o list - tedy uzel bez potomků). Typ NODETYPE je definován takto:
typedef enum NODETYPE {
NODE_TYPE,
LEAF_TYPE,
};
NODE_TYPE tedy představuje obyčejný uzel a LEAF_TYPE list. Dále uchováváme okrajové body uzlu. Tato informace se nám bude hodit při určování, zda-li je uzel uvnitř nebo vně Frustum. Proměnna pBraches je pole čtyř ukazatelů na potomky daného uzlu. Uzly na nejnižší úrovni nazýváme listy, to není nic nového a listy také uchovávají informaci o terénu. V našem případě se jedná přímo o Vertex buffer, což není zcela ideální, ale lépe to vyřešíme v příští lekci. Poslední atribut nám jen říká, zda-li je list vidět či nikoliv. Tuto vlastnost bychom ani nepotřebovali, ale chceme vykreslovat mapu viditelných listů (viz. dále). Na dalším obrázku vidíte význam většiny proměnných:
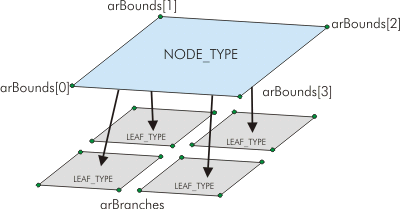
Obr. 3: Detail QTNode
Zelené kuličky v rozích představují body uložené v arBounds.
Přejděme k samotné třídě CTerrain:
class CTerrain
{
DWORD m_dwFlags;
// Common IB, heightmap and material
IIndexBuffer *m_pTerrainIB;
ITexture *m_pTerrainSurface;
ITexture *m_pHeightMap;
// Terrain dimensions
int m_iTerrainTilesX;
int m_iTerrainTilesY;
int m_iTerrainVerticesX;
int m_iTerrainVerticesY;
// Current terrain method
TERRAIN_METHOD m_iTerrainMethod;
I3DFont *m_pDebugFont;
std::vector <QTNode*> m_arLeaves;
std::vector <QTNode*> m_arVisQuads;
//
// Root of the quad tree
QTNode *m_pRoot;
//
// Vertices...
VERTEX **m_arTerrain;
//
// Common inicialization
HRESULT InternalInit();
int CreateNode(QTNode *pNode);
int FillLeaves();
int DestroyNode(QTNode *pNode);
int CircleAlgorithm();
int ComputeNormals();
int CreateQuadTree();
// Fills queue of the visible quads
HRESULT CullTerrain(QTNode *pNode, CLIPVOLUME& cv);
public:
HRESULT GenerateTerrain(int x, int y, TERRAIN_METHOD tmMethod = TM_CIRCLE);
HRESULT GenerateTerrainFromFile(LPCSTR szFile);
HRESULT DestroyTerrain();
int GetTitlesX() {return m_iTerrainTilesX;}
int GetTitlesY() {return m_iTerrainTilesY;}
void SetFlag(DWORD dwFlag) {m_dwFlags |= dwFlag;}
void UnsetFlag(DWORD dwFlag) {m_dwFlags &= ~dwFlag;}
void InvertFlag(DWORD dwFlag) { if(dwFlag & m_dwFlags) { UnsetFlag(dwFlag); } else { SetFlag(dwFlag);}}
void ResetFlags() {m_dwFlags = 0;}
HRESULT Render();
HRESULT Restore();
CTerrain(void);
~CTerrain(void);
};
V následující tabulce najdete popis metod:
Název |
Popis |
| GenerateTerrain(int x, int y, TERRAIN_METHOD tmMethod); | Generuje náhodný terén požadovanou metodou o daných rozměrech. Inicializuje proměnné m_iTerrainTilesX, m_iTerrainTilesY, m_iTerrainVerticesX, m_iTerrainVerticesY a vytvoří pole m_arTerrain. Ukládá metodu terénu: m_iTerrainMethod. |
| GenerateTerrainFromFile(LPCSTR szFile); | Generuje terén z heightmapy dané parametrem. Inicializuje proměnné m_iTerrainTilesX, m_iTerrainTilesY, m_iTerrainVerticesX, m_iTerrainVerticesY a vytvoří pole m_arTerrain. Dále načte heightmapu a ukazatel uloží do m_pHeightMap. Ukládá metodu terénu: m_iTerrainMethod. |
| DestroyTerrain(); | Odstraní terén z paměti (uvolní se všechny pomocné objekty, textury, VB a IB). |
| GetTitlesX() | Vrací velikost terénu ve směru x. |
| GetTitlesY() | Vrací velikost terénu ve směru y. |
| SetFlag(DWORD dwFlag) | Nastaví daný příznak. Modifikuje proměnnou m_dwFlags. |
| UnsetFlag(DWORD dwFlag) | Vynuluje příznak. Modifikuje proměnnou m_dwFlags. |
| InvertFlag(DWORD dwFlag) | Invertuje příznak. Modifikuje proměnnou m_dwFlags. |
| ResetFlags() | Vynuluje všechny příznaky. Modifikuje proměnnou m_dwFlags. |
| Render() | Provede oříznutí viditelných listů a vykreslí terén, případně mapu. Metoda by měla být volána v bloku BeginScene()-EndScene(). |
| Restore() | Obnoví všechny zdroje po ztrátě zařízení (textury, IB a VB jednotlivých listů). |
| InternalInit() | Alokuje některé zdroje společné pro oba typy tvorby terénu. Jedná se o texturu povrchu: m_pTerrainSurface, index buffer listů m_pTerrainIB a font m_pDebugFont. |
| CreateNode(QTNode *pNode) | Rekurzivní metoda vytvářející strukturu quad tree. |
| FillLeaves() | Naplní listy stromu daty, zkopíruje tedy vrcholy terénu do dílčích VB. |
| DestroyNode(QTNode *pNode) | Zcela uvolní paměť stromu tj. vymaže všechny uzle a listy i s jejich VB. |
| CircleAlgorithm() | Aplikuje algoritmus kopečků (viz. minulá lekce)). |
| ComputeNormals() | Spočítá normály celého terénu. Opět jsme tento postup probírali v minulé lekci. |
| CreateQuadTree() | Vytvoří celý quad tree. Nejprve tedy zinicializuje kořen stromu a poté spustí metody CreateNode(). |
| CullTerrain(QTNode *pNode, CLIPVOLUME& cv) | Zajistí ořezávání terénu tzn. naplní pole viditelných listů. |
Červeně jsou označeny soukromé metody. Nyní si ukážeme jednotlivé metody podrobněji.
Tvorba terénu:
HRESULT CTerrain::GenerateTerrainFromFile(LPCSTR szFile)
{
DWORD dwRet = S_FALSE;
int i = 0, x, y;
//
// Init common object (texture, font etc.)
InternalInit();
//
// Load heightmap texture
dwRet = CreateDisplayObject(DISIID_ITexture, (void**)&m_pHeightMap);
if(dwRet == S_OK)
{
dwRet = m_pHeightMap->LoadTextureFromFile(szFile);
if(dwRet != S_OK)
{
XException exp("Cannot load texture for heightmap!", dwRet);
THROW(exp);
}
if(m_pHeightMap->GetFormat() != D3DFMT_A8R8G8B8 && m_pHeightMap->GetFormat() != D3DFMT_X8R8G8B8)
{
XException exp("Invalid heightmap format! Must be 32-bit with alpha channel.");
THROW(exp);
}
//set dim of the terrain according dim of the height map
m_iTerrainTilesX = m_pHeightMap->Width() - 1;
m_iTerrainTilesY = m_pHeightMap->Height() - 1;
m_iTerrainVerticesX = m_pHeightMap->Width();
m_iTerrainVerticesY = m_pHeightMap->Height();
}
m_arTerrain = new VERTEX*[m_iTerrainVerticesX];
for(i = 0; i < m_iTerrainVerticesX; i++)
{
m_arTerrain[i] = new VERTEX[m_iTerrainVerticesY];
}
//
// Open heightmap
D3DLOCKED_RECT lr;
m_pHeightMap->GetTexture()->LockRect(0, &lr, NULL, D3DLOCK_READONLY);
TEXTURE_PIXEL * data = (TEXTURE_PIXEL*)lr.pBits;
int p = lr.Pitch/4;
// Init basic terrain parameters
for(y = 0; y < m_iTerrainVerticesY; y++)
{
for(x = 0; x < m_iTerrainVerticesX; x++)
{
TEXTURE_PIXEL tp = data[y*p + x];m_arTerrain[x][y].vecPos = D3DXVECTOR3(float(x), float(y), float(tp.a)/255.0f*20.0f-10.0f);
m_arTerrain[x][y].dwDiffuse = D3DCOLOR_ARGB(128, tp.r, tp.g, tp.b);
m_arTerrain[x][y].tu1 = (x % 2) ? 1.0f : 0.0f;
m_arTerrain[x][y].tv1 = (y % 2) ? 1.0f : 0.0f;
m_arTerrain[x][y].vecNormal = D3DXVECTOR3(0.0f, 0.0f, 1.0f);
}
}
m_pHeightMap->GetTexture()->UnlockRect(0);ComputeNormals();
//
// Create quad tree
CreateQuadTree();return dwRet;
}
Jak jsem již zmínil, tato metoda vytvoří terén z heightmapy. Prakticky shrnuje vše, co jsme napsali v minulé lekci. Nejprve vytvoříme společné objekty jako je font nebo textura povrchu, pak načteme texturu heightmapy do paměti, vytvoříme 2D pole terénu a naplníme ho daty podle textury. Nakonec spočteme normály a vytvoříme strom.
HRESULT CTerrain::GenerateTerrain(int x, int y, TERRAIN_METHOD tmMethod /*= TM_CIRCLE*/)
{
DWORD dwRet = S_FALSE;
int i = 0;
//
// Init common object (texture, font etc.)
InternalInit();m_iTerrainTilesX = x;
m_iTerrainTilesY = y;
m_iTerrainVerticesX = x + 1;
m_iTerrainVerticesY = y + 1;
m_arTerrain = new VERTEX*[m_iTerrainVerticesX];
for(i = 0; i < m_iTerrainVerticesX; i++)
{
m_arTerrain[i] = new VERTEX[m_iTerrainVerticesY];
}
//
// Init basic terrain parameters
for(y = 0; y < m_iTerrainVerticesY; y++)
{
for(x = 0; x < m_iTerrainVerticesX; x++)
{
m_arTerrain[x][y].vecPos = D3DXVECTOR3(float(x), float(y), 0.0f);
m_arTerrain[x][y].dwDiffuse = D3DCOLOR_ARGB(128,128,255,128);
m_arTerrain[x][y].tu1 = (x % 2) ? 1.0f : 0.0f;
m_arTerrain[x][y].tv1 = (y % 2) ? 1.0f : 0.0f;
m_arTerrain[x][y].vecNormal = D3DXVECTOR3(0.0f, 0.0f, 1.0f);
}
}
//
// Apply circle algorithm on the terrain
CircleAlgorithm();
ComputeNormals();
//
// Create quad tree
CreateQuadTree();
return dwRet;
}
Tato metoda je podobná, opět se volá metoda InternalInit() a pak se vytvoří 2D pole vertexů, které se naplní daty. Použije se algoritmus kopečků a spočítají se normály. Na závěr postavíme strom. V předchozích metodách také ukládáme velikost terénu. V prvním případě se bere podle velikost textury heightmapy. Ve druhém je pak dána dvěma parametry.
Protože s přípravou terénu úzce souvisí metoda InternalInit(), podívejme se teď na ní:
HRESULT CTerrain::InternalInit()
{
DWORD dwRet = S_FALSE;
DWORD dwTerrainIBSize, dwIndicesCount;
IDisplay *pDis;
CreateDisplayObject(DISIID_IDisplay, (void**) &pDis);
//
// Create font
if(S_OK == (dwRet = CreateDisplayObject(DISIID_I3DFont, (void**) &m_pDebugFont)))
{
m_pDebugFont->CreateFont(15, 8, "Arial", TRUE, D3DCOLOR_ARGB(255,150,255,100));
}
else
{
TRACE("Cannot create font: %d", dwRet);
return dwRet;
}
//
// Create common index buffer for all quad leaves
dwRet = CreateDisplayObject(DISIID_IIndexBuffer, (void**) &m_pTerrainIB);
if(dwRet == S_OK)
{
dwTerrainIBSize = LEAF_I_SIZE * LEAF_I_SIZE * 6 * sizeof(WORD);
dwIndicesCount = LEAF_I_SIZE * LEAF_I_SIZE * 6;
dwRet = m_pTerrainIB->Create(dwTerrainIBSize, D3DUSAGE_WRITEONLY, D3DFMT_INDEX16, D3DPOOL_DEFAULT);
if(dwRet != S_OK)
{
XException exp("Cannot create IB for terrain!", dwRet);
THROW(exp);
}
}//
// Load terrain texture
dwRet = CreateDisplayObject(DISIID_ITexture, (void**)&m_pTerrainSurface);
if(dwRet == S_OK)
{
dwRet = m_pTerrainSurface->LoadTextureFromFileEx("grass64.bmp", 6, pDis->GetTextureFormat());
if(dwRet != S_OK)
{
XException exp("Cannot load texture for terrain surface!", dwRet);
THROW(exp);
}
}SAFE_RELEASE(pDis);
return dwRet;
}
Nejedná se o nic složitého, protože metoda má jen za úkol vytvořit pár objektů: font, kterým píšeme informace o terénu na obrazovku, index buffer jednoho listu, který využijeme při vykreslování a textura povrchu terénu - naše známá tráva.
Veledůležitou metodou a vlastně podstatou je CreateNode(). Tato metoda je rekurzivní tzn. že volá sama sebe pro každý uzel stromu. Začínáme od kořene v metodě CreateQuadTree():
int CTerrain::CreateQuadTree()
{
//
// Check terrain validity
if(!m_arTerrain)
{
XException exp("Terrain is not initialized. You cannot apply any algorithm.");
THROW(exp);
}
if(m_iTerrainVerticesX >= LEAF_I_SIZE && m_iTerrainVerticesY >= LEAF_I_SIZE)
{
m_pRoot = new QTNode;
// Init ROOT
m_pRoot->ntType = NODE_TYPE;
m_pRoot->pVB = NULL;
m_pRoot->arBounds[0].x = m_arTerrain[0][0].vecPos.x;
m_pRoot->arBounds[0].y = m_arTerrain[0][0].vecPos.y;
m_pRoot->arBounds[0].z = m_arTerrain[0][0].vecPos.z;
m_pRoot->arBounds[1].x = m_arTerrain[m_iTerrainVerticesX-1][0].vecPos.x;
m_pRoot->arBounds[1].y = m_arTerrain[m_iTerrainVerticesX-1][0].vecPos.y;
m_pRoot->arBounds[1].z = m_arTerrain[m_iTerrainVerticesX-1][0].vecPos.z;
m_pRoot->arBounds[2].x = m_arTerrain[0][m_iTerrainVerticesY-1].vecPos.x;
m_pRoot->arBounds[2].y = m_arTerrain[0][m_iTerrainVerticesY-1].vecPos.y;
m_pRoot->arBounds[2].z = m_arTerrain[0][m_iTerrainVerticesY-1].vecPos.z;
m_pRoot->arBounds[3].x = m_arTerrain[m_iTerrainVerticesX-1]
[m_iTerrainVerticesY-1].vecPos.x;
m_pRoot->arBounds[3].y = m_arTerrain[m_iTerrainVerticesX-1]
[m_iTerrainVerticesY-1].vecPos.y;
m_pRoot->arBounds[3].z = m_arTerrain[m_iTerrainVerticesX-1]
[m_iTerrainVerticesY-1].vecPos.z;CreateNode(m_pRoot);
//
// Fill index buffer and leaves with data
Restore();
}
else
{
return S_FALSE;
}
return S_OK;
}
Zde tedy připravíme první uzel - kořen - a zavoláme CreateNode(). Na závěr naplníme všechny listy daty pomocí metody Restore(). Všimněte si inicializace okrajových bodů. Jednoduše použijeme krajní body pole m_arTerrain, protože kořen je přes celý terén, uzel s největší rozlohou.
int CTerrain::CreateNode(QTNode *pNode)
{
UINT uiWidth, uiHeight;
//
// Check terrain validity
if(!m_arTerrain)
{
XException exp("Terrain is not initialized. You cannot apply any algorithm.");
THROW(exp);
}
if(pNode)
{//
// Compute node width and height
uiWidth = int(pNode->arBounds[1].x - pNode->arBounds[0].x);
uiHeight = int(pNode->arBounds[2].y - pNode->arBounds[0].y);
//
// Get node type
if(uiWidth == LEAF_I_SIZE)
{
pNode->ntType = LEAF_TYPE;
// Create vertex buffer
if(S_OK == CreateDisplayObject(DISIID_IVertexBuffer, (void**) &pNode->pVB))
{
pNode->pVB->Create(LEAF_V_SIZE*LEAF_V_SIZE*sizeof(VERTEX),
D3DUSAGE_WRITEONLY, VERTEXFORMAT, D3DPOOL_DEFAULT);
pNode->bVis = FALSE;
m_arLeaves.push_back(pNode);
}
return 1;
}
else
{pNode->ntType = NODE_TYPE;
//
// Create 4 children// First
pNode->pBranches[0] = new QTNode;
pNode->pBranches[0]->pVB = NULL;
// Init new bounding box
pNode->pBranches[0]->arBounds[0] = pNode->arBounds[0];pNode->pBranches[0]->arBounds[1].x = pNode->arBounds[1].x - uiWidth / 2;
pNode->pBranches[0]->arBounds[1].y = pNode->arBounds[1].y;
pNode->pBranches[0]->arBounds[1].z = m_arTerrain[int(pNode->pBranches[0]->arBounds[1].x)]
[int(pNode->pBranches[0]->arBounds[1].y)].vecPos.z;pNode->pBranches[0]->arBounds[2].x = pNode->arBounds[2].x;
pNode->pBranches[0]->arBounds[2].y = pNode->arBounds[2].y - uiHeight / 2;
pNode->pBranches[0]->arBounds[2].z = m_arTerrain[int(pNode->pBranches[0]->arBounds[2].x)](
[int(pNode->pBranches[0]->arBounds[2].y)].vecPos.z;pNode->pBranches[0]->arBounds[3].x = pNode->arBounds[3].x - uiWidth / 2;
pNode->pBranches[0]->arBounds[3].y = pNode->arBounds[3].y - uiHeight / 2;
pNode->pBranches[0]->arBounds[3].z = m_arTerrain[int(pNode->pBranches[0]->arBounds[3].x)]
[int(pNode->pBranches[0]->arBounds[3].y)].vecPos.z;
// Second
pNode->pBranches[1] = new QTNode;
pNode->pBranches[1]->pVB = NULL;
// Init new bounding box
pNode->pBranches[1]->arBounds[0].x = pNode->arBounds[0].x + uiWidth / 2;
pNode->pBranches[1]->arBounds[0].y = pNode->arBounds[0].y;
pNode->pBranches[1]->arBounds[0].z = m_arTerrain[int(pNode->pBranches[1]->arBounds[0].x)]
[int(pNode->pBranches[1]->arBounds[0].y)].vecPos.z;pNode->pBranches[1]->arBounds[1] = pNode->arBounds[1];
pNode->pBranches[1]->arBounds[2].x = pNode->arBounds[2].x + uiWidth / 2;
pNode->pBranches[1]->arBounds[2].y = pNode->arBounds[2].y - uiHeight / 2;
pNode->pBranches[1]->arBounds[2].z = m_arTerrain[int(pNode->pBranches[1]->arBounds[2].x)]
[int(pNode->pBranches[1]->arBounds[2].y)].vecPos.z;pNode->pBranches[1]->arBounds[3].x = pNode->arBounds[3].x;
pNode->pBranches[1]->arBounds[3].y = pNode->arBounds[3].y - uiHeight / 2;
pNode->pBranches[1]->arBounds[3].z = m_arTerrain[int(pNode->pBranches[1]->arBounds[3].x)]
[int(pNode->pBranches[1]->arBounds[3].y)].vecPos.z;// Third
pNode->pBranches[2] = new QTNode;
pNode->pBranches[2]->pVB = NULL;
// Init new bounding box
pNode->pBranches[2]->arBounds[0].x = pNode->arBounds[0].x;
pNode->pBranches[2]->arBounds[0].y = pNode->arBounds[0].y + uiHeight / 2;
pNode->pBranches[2]->arBounds[0].z = m_arTerrain[int(pNode->pBranches[2]->arBounds[0].x)]
[int(pNode->pBranches[2]->arBounds[0].y)].vecPos.z;
pNode->pBranches[2]->arBounds[1].x = pNode->arBounds[1].x - uiWidth / 2;
pNode->pBranches[2]->arBounds[1].y = pNode->arBounds[1].y + uiHeight / 2;
pNode->pBranches[2]->arBounds[1].z = m_arTerrain[int(pNode->pBranches[2]->arBounds[1].x)]
[int(pNode->pBranches[2]->arBounds[1].y)].vecPos.z;pNode->pBranches[2]->arBounds[2] = pNode->arBounds[2];
pNode->pBranches[2]->arBounds[3].x = pNode->arBounds[3].x - uiWidth / 2;
pNode->pBranches[2]->arBounds[3].y = pNode->arBounds[3].y;
pNode->pBranches[2]->arBounds[3].z = m_arTerrain[int(pNode->pBranches[2]->arBounds[3].x)]
[int(pNode->pBranches[2]->arBounds[3].y)].vecPos.z;// Fourth
pNode->pBranches[3] = new QTNode;
pNode->pBranches[3]->pVB = NULL;
// Init new bounding box
pNode->pBranches[3]->arBounds[0].x = pNode->arBounds[0].x + uiWidth / 2;
pNode->pBranches[3]->arBounds[0].y = pNode->arBounds[0].y + uiHeight / 2;
pNode->pBranches[3]->arBounds[0].z = m_arTerrain[int(pNode->pBranches[3]->arBounds[0].x)]
[int(pNode->pBranches[3]->arBounds[0].y)].vecPos.z;
pNode->pBranches[3]->arBounds[1].x = pNode->arBounds[1].x;
pNode->pBranches[3]->arBounds[1].y = pNode->arBounds[1].y + uiHeight / 2;
pNode->pBranches[3]->arBounds[1].z = m_arTerrain[int(pNode->pBranches[3]->arBounds[1].x)]
[int(pNode->pBranches[3]->arBounds[1].y)].vecPos.z;pNode->pBranches[3]->arBounds[2].x = pNode->arBounds[2].x + uiWidth / 2;
pNode->pBranches[3]->arBounds[2].y = pNode->arBounds[2].y;
pNode->pBranches[3]->arBounds[2].z = m_arTerrain[int(pNode->pBranches[2]->arBounds[2].x)]
[int(pNode->pBranches[3]->arBounds[2].y)].vecPos.z;pNode->pBranches[3]->arBounds[3] = pNode->arBounds[3];
// Create children of the children
CreateNode(pNode->pBranches[0]);
CreateNode(pNode->pBranches[1]);
CreateNode(pNode->pBranches[2]);
CreateNode(pNode->pBranches[3]);}
return 0;}
return -1;
}
Metoda vypadající na první pohled složitě. Na druhý je to úplně jednoduché. Nejprve potřebujeme spočítat velikost aktuálního uzlu (tj. uzlu, pro který byla metoda volána). Otec tohoto uzlu ovšem pro nás spočítal okrajové body, stačí tedy od sebe odečíst ty správné dva a dostaneme tak šířku uiWidth a "výšku" uiHeight uzlu. Dále testujeme, zda-li jsme již nedosáhli nejnižší "listové" úrovně. Velikost listu definuje konstanta LEAF_I_SIZE. Pokud ano, aktuální uzel je list a provedeme tři operace: uzel si musí pamatovat, že je list, vytvoří se pro něj vertex buffer (zatím se neplní) a vloží se do pole listů - v tomto bodě je metoda ukončena a vracíme se o úroveň výš.
Pokud je ale uzel ještě příliš velký, je třeba ho znovu rozčtvrtit a pro každou čtvrtinu zavolat CreateNode(). Takže vytvoříme čtyři nové uzly a nastavíme jim nové krajní body tak, aby pokryly předcházející uzel. Tohle si určitě nakreslete na kousek papíru!
Listy máme uloženy v poli m_arLeaves a nyní je musíme naplnit daty z hlavního pole celého terénu m_arTerrain:
int CTerrain::FillLeaves()
{
QTNode *pNode;
VERTEX *pVertices;
int v, y, x, i;
for(i = 0; i < (int)m_arLeaves.size(); i++)
{
pNode = (QTNode*)m_arLeaves[i];
pNode->pVB->GetBuffer()->Lock(0, 0, (BYTE**) &pVertices, 0);
v = 0;
for(y = (int)pNode->arBounds[0].y; y <= (int)pNode->arBounds[2].y; y++)
{
for(x = (int)pNode->arBounds[0].x; x <= (int)pNode->arBounds[1].x; x++)
{
pVertices[v] = m_arTerrain[x][y];
v++;
}
}
pNode->pVB->GetBuffer()->Unlock();
}
return -1;
}
Zbývá metoda pro naplnění a obnovu Vertex a Index bufferu. Při ztrátě zařízení (a i při inicializaci) se automatický volá metoda Restore(), která naplní IB a volá metodu pro naplnění všech listů:
HRESULT CTerrain::Restore() if(m_arTerrain)
{
TRACE("Restoring terrain surface...");
dwRet = m_pTerrainIB->GetBuffer()->Lock(0, 0, (BYTE**)&pIndices, 0);
for(y = 0; y < LEAF_I_SIZE; y++)
{
for(x = 0; x < LEAF_I_SIZE; x++)
{
pIndices[i + 0] = x + y * LEAF_V_SIZE;
pIndices[i + 1] = (x+1) + y * LEAF_V_SIZE;
pIndices[i + 2] = x + (y+1) * LEAF_V_SIZE;
i += 3;
pIndices[i + 0] = (x+1) + y * LEAF_V_SIZE;
pIndices[i + 1] = (x+1) + (y+1) * LEAF_V_SIZE;
pIndices[i + 2] = x + (y+1) * LEAF_V_SIZE;
i += 3;
}
}
dwRet = m_pTerrainIB->GetBuffer()->Unlock();
dwRet = FillLeaves();
}
return dwRet;
}
V Index bufferu jsou odkazy v rámci jednoho listu, protože listy budeme vykreslovat postupně. Princip naleznete v minulé lekci - je to jako kdybychom měli malý povrch o rozměrech jednoho listu.
Nyní si ukážeme jak ořezávat listy, které jsou mimo Frustum. Ořezávání se provádí v metodě CullTerrain(). Jedná se opět o rekurzivní metodu (všimněte si, že pokud pracujeme se stromem, rekurze nám podstatně zjednodušuje život). Výsledek metody je seznam viditelných listů:
// Fills queue of the visible quads
HRESULT CTerrain::CullTerrain(QTNode *pNode, CLIPVOLUME& cv)
{
DWORD zones[4] = {0, 0, 0, 0};
FLOAT x, y, z;
float temp;
for(int i = 0; i < 4; i++)
{
x = pNode->arBounds[i].x;
y = pNode->arBounds[i].y;
z = pNode->arBounds[i].z;
temp = cv.pNear.a * x + cv.pNear.b * y + cv.pNear.c * z + cv.pNear.d;
if (temp > CULL_TOLERANCE) {
zones[i] |= 0x01;
}
else {
temp = cv.pFar.a * x + cv.pFar.b * y + cv.pFar.c * z + cv.pFar.d;
if (temp > CULL_TOLERANCE) {
zones[i] |= 0x02;
}
}
temp = cv.pLeft.a * x + cv.pLeft.b * y + cv.pLeft.c * z + cv.pLeft.d;
if (temp > CULL_TOLERANCE) {
zones[i] |= 0x04;
}
else {
temp = cv.pRight.a * x + cv.pRight.b * y + cv.pRight.c * z + cv.pRight.d;
if (temp > CULL_TOLERANCE) {
zones[i] |= 0x08;
}
}
temp = cv.pTop.a * x + cv.pTop.b * y + cv.pTop.c * z + cv.pTop.d;
if (temp > CULL_TOLERANCE+2.0f) {
zones[i] |= 0x10;
}
else
{
temp = cv.pBottom.a * x + cv.pBottom.b * y + cv.pBottom.c * z + cv.pBottom.d;
if (temp > CULL_TOLERANCE) {
zones[i] |= 0x20;
}
}
}
//if all of the corners are outside of the boundaries
// this node is excluded, so stop traversing
DWORD res = zones[0] & zones[1] & zones[2] & zones[3];
if(res)
{
return -1;
}
// if this is a leaf add the triangle lists to the render queue
if (pNode->ntType == LEAF_TYPE)
{
pNode->bVis = TRUE;
m_arVisQuads.push_back(pNode);
return 1;
}
else
{
//this is not a leaf traverse deeper
for(i = 0; i < 4; i++) {
CullTerrain(pNode->pBranches[i], cv);
}
}
return 0;
}
Princip metody spočívá v tom, že zkoumáme všechny čtyři krajní body každého uzlu a testujeme, zda-li jsou uvnitř Frustum nebo ne. Pokud je alespoň jeden bod uvnitř, považujeme uzel za viditelný a pokud se jedná o list, přidáme ho do pole m_arVisQuads. V opačném případě voláme metody CullTerrain() pro všechny potomky.
Ještě se vrátím k testu. Zde konečně využijeme naší novou strukturu CLIPVOLUME. Postupně vezmeme všechny stěny Frustum a dosazujeme krajní body uzlu. Pokud by bod ležel přesně v rovině (což se ve světe floatů prakticky nemůže stát), vyšel by výsledek 0. Nás ale zajímá situace, kdy je bod venku (uvnitř). Pak vyjde výsledek kladný (v našem případě používáme konstantu CULL_TOLERANCE, pomocí které můžeme řídit přesah) a to zaznamenáme v poli zones, kam se postupně přidává informace o bodech, které jsou mimo. Pokud jsou mimo všechny, metoda se ukončí.
Na závěr si ještě ukážeme vykreslovací metodu Render().
HRESULT CTerrain::Render()
{
IDisplay *pDis;
CLIPVOLUME cv;
PIXEL v;
int i;
char szInfo[255];
CreateDisplayObject(DISIID_IDisplay, (void**) &pDis);if(m_dwFlags & TF_DRAWQUADSMAP)
{
for(i = 0; i < (int)m_arLeaves.size(); i++)
{
((QTNode*)m_arLeaves[i])->bVis = FALSE;
}
}m_arVisQuads.clear();
pDis->GetCamera()->GetClipVolume(cv);
CullTerrain(m_pRoot, cv);pDis->GetDevice()->SetVertexShader(VERTEXFORMAT);
pDis->GetDevice()->SetIndices(m_pTerrainIB->GetBuffer(), 0);
pDis->GetDevice()->SetTexture(0, m_pTerrainSurface->GetTexture());if(m_dwFlags & TF_USEQUADS)
{
for(i = 0; i < (int)m_arVisQuads.size(); i++)
{
pDis->GetDevice()->SetStreamSource(0,((QTNode*)m_arVisQuads[i])->pVB->GetBuffer(),
sizeof(VERTEX));
pDis->GetDevice()->DrawIndexedPrimitive(D3DPT_TRIANGLELIST,0,LEAF_V_SIZE*LEAF_V_SIZE,0,
LEAF_I_SIZE*LEAF_I_SIZE * 2);
}
sprintf(szInfo, "Using quad tree culling\nTotal leaves: %d\nTotal faces: %d",
(int)m_arVisQuads.size(),(int)m_arVisQuads.size() * LEAF_I_SIZE * LEAF_I_SIZE * 2);
}
else
{
for(i = 0; i < (int)m_arLeaves.size(); i++)
{
pDis->GetDevice()->SetStreamSource(0, ((QTNode*)m_arLeaves[i])->pVB->GetBuffer(),
sizeof(VERTEX));
pDis->GetDevice()->DrawIndexedPrimitive(D3DPT_TRIANGLELIST,0,LEAF_V_SIZE*LEAF_V_SIZE,0, LEAF_I_SIZE*LEAF_I_SIZE * 2);
}
sprintf(szInfo, "Without quad tree culling\nTotal leaves: %d\nTotal faces: %d",
(int)m_arLeaves.size(), (int)m_arLeaves.size() * LEAF_I_SIZE * LEAF_I_SIZE * 2);
}if(m_dwFlags & TF_DRAWQUADSMAP)
{
pDis->GetDevice()->SetVertexShader(PIXELFORMAT);
pDis->GetDevice()->SetRenderState(D3DRS_LIGHTING, FALSE);
pDis->GetDevice()->SetTexture(0, NULL);
for(i = 0; i < (int)m_arLeaves.size(); i++)
{
QTNode *pNode = (QTNode*)m_arLeaves[i];
v.vecPos.x = pNode->arBounds[0].x/LEAF_I_SIZE +
pDis->GetResolution()->x - m_iTerrainTilesX/LEAF_I_SIZE - 10;
v.vecPos.y = pNode->arBounds[0].y/LEAF_I_SIZE + 10;
v.vecPos.z = 0.0f;
v.rhw = 1.0f;
if(pNode->bVis)
{
v.dwDiffuse = D3DCOLOR_ARGB(255,255,255,0);
}
else
{
v.dwDiffuse = D3DCOLOR_ARGB(255,128,128,128);
}
pDis->GetDevice()->DrawPrimitiveUP(D3DPT_POINTLIST, 1, &v, sizeof(PIXEL));
}
pDis->GetDevice()->SetRenderState(D3DRS_LIGHTING, TRUE);
}
m_pDebugFont->Draw(szInfo, 0, 300);SAFE_RELEASE(pDis);
return 0;
}
Pokud máme aktivní mapu, je třeba vymazat viditelnost všech listů. V opačném případě atribut bVis vůbec k ničemu nepoužíváme, takže tuto smyčku můžeme přeskočit. Dále použijeme objekt CLIPVOLUME z naší kamery a provedeme ořezání metodou CullTerrain().
Před vykreslením musíme nastavit známé parametry jako formát vertexů, texturu a index bufferu. Poté se rozhoduje, jakým způsobem budeme listy vykreslovat. Pokud je zapnutá optimalizace, vykreslují se pouze viditelné listy z pole m_arVisQuads. V opačném případě se vykreslí všechny listy z pole m_arLeaves.
V poslední části vykreslujeme mapu (pokud o to uživatel stojí). Mapa je tvořena v pravém horním rohu a zatím ji vykreslujeme po pixelech. každý pixel představuje list. Viditelné jsou žluté, ostatní šedé. Používáme k tomu transformované vrcholy PIXEL, u nichž nastavujeme pouze polohu (přímo v souřadnicích obrazovky) a barvu.
Na závěr vykreslíme informace o terénu. Vypisuje se pouze počet viditelných listů a celkový počet polygonů.
A co nás čeká v příští lekci? Dále budeme zdokonalovat náš jednoduchý engine. Například přidáme oblohu a podíváme se, jak dále upravit a zrychlit vykreslovaní terénu (optimalizovat lze téměř donekonečna). Dále bych chtěl vylepšit podporu světel. Budou to tedy spíše takové "kosmetické" změny než revoluce, kterou jste viděli dnes.
Těším se příště nashledanou.