V minulΘ lekci jsme zakonΦili ukßzkov² p°φklad DirectDraw, DirectInput a DirectMusic. V dneÜnφ lekci opustφme vÜechna tato tΘmata a vrhneme se na zcela novou lßtku. Dnes a v n∞kolika (v mnoha) p°φÜtφch lekcφch se budeme zab²vat komponentou Direct3D.
Je tomu skuteΦn∞ tak! P°esuneme se od 2D zobrazovßnφ do 3D sv∞ta. V dneÜnφ lekci jeÜt∞ nebudeme nic programovat, ale povφme si n∞kterΘ zßklady, kterß dßle vyu₧ijeme.
Narozdφl od DirectDraw mß Direct3D mnohem rozsßhlejÜφ hardwarovou i softwarovou podporu. DirectDraw zaniklo, ale Direct3D mß svojφ cestu p°ed sebou (dneÜnφ hry jsou p∞knΘ, ale k dokonalosti majφ opravdu daleko).
Mo₧nß jste si na internetu vÜimli, ₧e ji₧ vyÜla novß verze DirectX a s nφ i novΘ DirectX SDK 9.0. Bohu₧el toto SDK nem∙₧eme zahrnout na ChipCD, proto₧e je n∞kolikanßsobn∞ v∞tÜφ ne₧ SDK p°edchozφ verze. Ve sv²ch lekcφch tedy budu pou₧φvat "starΘ" SDK 8.0 Φi 8.1. Pokud by se to n∞komu nelφbilo, tak v∞zte, ₧e verze 9.0 mß pro nßs n∞kolik kosmetick²ch zm∞n. DirectX SDK 8.0 bylo uvedeno na ChipCD v listopadu roku 2001. NovΘ SDK si m∙₧ete stßhnout p°φmo z Microsoftu, ale velikost 100MB je pro vytßΦenΘ p°ipojenφ opravdu hodn∞ (i kdy₧ znßm takovΘ Üφlence).
Nejprve si n∞co povφme o struktu°e Direct3D.
18.1.1. Pipeline Direct3D
Na nßsledujφcφm obrßzku vidφte architekturu systΘmu Direct3D. Je to vlastn∞ cesta vstupnφch dat (vertex∙ - viz. dßle) a₧ po vykreslenφ do zobrazovanΘ pam∞ti grafickΘ karty.
Co d∞lajφ jednotlivΘ bloky zatφm nenφ t°eba znßt, ale postupn∞ se k nim dostaneme dostateΦn∞ podrobn∞ji. Obrßzek zde uvßdφm, abyste si ud∞lali celkovou p°edstavu o systΘmu a pak aby si n∞kdo nemyslel, ₧e nejprve nanese texturu a potΘ transformuje vertexy. O Φem to tu vlastn∞ hovo°φm? Nechte se p°ekvapit (teda pokud o tom skuteΦn∞ nic nevφte a jste jen pasivnφm u₧ivatelem Direct3D).
V dalÜφ Φßsti si n∞co povφme o 3D prostoru, kter² mßme k dispozici.
18.1.2. 3D prostor v Direct3D
Direct3D vyu₧φvß klasick² kartΘzsk² (pravo·hl²) systΘm se t°emi osami x, y a z. Existujφ dva typy t∞chto sou°adnicov²ch systΘm∙, kterΘ se liÜφ ve sm∞ru osy z. K urΦenφ sm∞ru osy si pomßhßme rukou. VÜechny prsty krom∞ palce majφ v₧dy sm∞r osy y, ruka mφ°φ po sm∞ru osy x a palec pak urΦuje kladn² sm∞r osy z. Te∩ jde o to jakou ruku pou₧ijete a podle toho d∞lφme systΘmy na systΘm levΘ a pravΘ ruky. Direct3D pou₧φvß systΘm s levou rukou (obrßzek vlevo). Sm∞r os ale m∙₧ete prohßzet, tak₧e nap°φklad m∙₧ete prohodit y a z (co₧ osobn∞ pou₧φvßm jß).
VÜe je vid∞t na dalÜφm obrßzku:
Poznßmka: Kdo pou₧φvß nßpov∞du MSDN, tak tyto obrßzky jsem pou₧il z nφ.
18.1.3. Vertex
Ji₧ n∞kolikrßt zde padlo toto slovo. Vertex je do ΦeÜtiny p°elo₧en² vrchol. Budu zde ovÜem p°evß₧n∞ u₧φvat anglickΘho tvaru, proto₧e se mi lφbφ vφc. Ka₧d² objekt ve sv∞t∞ Direct3D je tvo°en polygony. KonkrΘtn∞ jsou pou₧ity troj·helnφky, proto₧e jsou tzv. koplanßrnφ (jsou rovinnΘ). T°i vrcholy tedy tvo°φ dohromady jeden troj·helnφk. Pozd∞ji vÜak zjistφte, ₧e vertexy mohou b²t spoleΦnΘ pro vφce troj·helnφk∙. Kdybychom m∞li 4 vertexy, vytvo°ili bychom obdΘlnφk, tφm by ale nebyla jednoznaΦn∞ definovanß rovina, proto₧e tento obdΘlnφk by Üel "zlomit" (vznikly by tak dv∞ roviny). Tak₧e z troj·helnφk∙ m∙₧eme slo₧it libovoln² tvar, i kdy₧ se to mo₧nß na prvnφ pohled nezdß. Uka₧me si n∞kolik p°φklad∙ 3D t∞les. Jednoduchß kostka mß 6 stran a ka₧dß obsahuje dva troj·helnφky:
Dßle vidφme kouli slo₧enou z mnoha troj·helnφk∙:
Abychom docφlili dokonale kulatΘ koule, museli bychom ji sestavit z nekoneΦnΘho mno₧stvφ troj·helnφk∙. TakovΘ mno₧stvφ polygon∙ by se ovÜem nelφbilo vaÜφ grafickΘ kart∞. V praxi docφlφme kulatosti pomocφ pßr troj·helnφk∙.
Ka₧d² vertex mß svou pozici v prostoru urΦenou polohov²m vektorem r. Tento vektor mß t°i sou°adnice x, y a z. Vertex dßle m∙₧e obsahovat barvu, texturovΘ sou°adnice, normßlov² vektor atd. Vertexovß data jsou p°evß₧n∞ naΦφtßna z externφch soubor∙ s p°φponou .x nebo .3ds. Soubory 3DS vytvß°φ 3D Studio MAX, tak₧e nenφ problΘm nakreslit objekt v tomto prost°edφ a pak ho p°enΘst do vaÜeho programu. Je vÜak t°eba rozluÜtit 3DS soubor, co₧ ale nenφ takov² problΘm. Myslφm, ₧e existuje n∞jak² plugin do 3D Studia na export do .x soubor∙.
18.1.4. Zpracovßnφ vertex∙
Nynφ si povφme, co s vertexy provede vaÜe grafickß karta, p°φpadn∞ procesor p°ed zobrazenφm na monitoru. Pozice vertexu je toti₧ v sou°adnicφch vaÜeho 3D prostoru a je t°eba ji transformovat, aby bylo mo₧nΘ vertex zobrazit na monitoru. Podφvßte-li se jeÜt∞ jednou na obrßzek pipeline, tak se nynφ bavφme o Φßstech Fixed Function pipeline a Programmable pipeline. Dß se °φci, ₧e v Direct3D mßme t°i zp∙soby zpracovßnφ vertex∙ (vertex proccessing). Za prvΘ m∙₧eme pracovat s tzv. transformovan²mi vertexy (transformed vertices), kterΘ v²Üe uveden²mi bloky v∙bec neprojdou. Tyto vertexy majφ danou pozici jako kdyby to byly sprity s DirectDraw a takΘ na tyto ·Φely se dajφ pou₧φt (kurzor myÜi, tlaΦφtka menu, okna apod.). V dalÜφ Φßsti se ji₧ budeme zab²vat jen netransformovan²mi vertexy (untransformed vertices). P°φÜt∞ si vytvo°φme prvnφ program Direct3D, kde si ukß₧eme prßci s transformovan²mi vertexy.
DalÜφm druhem zpracovßnφ je uvedena Fixed function pipeline. Na ka₧d² vertex je provedena transformace t°φ matic - sv∞tovΘ, matice pohledu a projekΦnφ matice. O transformacφch pomocφ matic se zmφnφm podrobn∞ pozd∞ji. Nynφ vßm staΦφ v∞d∞t, ₧e tento zp∙sob byl pou₧φvßn nejΦast∞ji v minulosti v DirectX 7.0. V dneÜnφ dob∞ ji₧ mßte mo₧nost volby, i kdy₧ se tento zp∙sob samoz°ejm∞ pou₧φvß stßle. Fixed function se °φkß proto, ₧e vy jako₧to programßtor nem∙₧ete ovlivnit pr∙b∞h transformace - prost∞ na zaΦßtku programu nastavφte v²Üe uvedenΘ matice a o vÜe ostatnφ se postarß Direct3D (pro n∞koho to m∙₧e b²t v²hoda). Ze zaΦßtku tento systΘm budeme hodn∞ pou₧φvat a vlastn∞ se ho nikdy ·pln∞ nevzdßme.
S DirectX 8.0 ovÜem p°iÜel v tomto ohledu zlom. Stejn² zlom samoz°ejm∞ zaznamenal i hardware. Jednß se o programovatelnΘ zpracovßnφ vertex∙. Blok ve kterΘm se tyto operace provßd∞jφ se naz²vß vertex shader a Φasem se k n∞mu takΘ dostaneme. Pomocφ tohoto prost°edku napφÜete krßtk² (max. 128 instrukcφ u nVidia GeForce, 192 u ATI Radeon) k≤d assembleru. Nejednß se o klasick² assembler, ale o assembler specißln∞ urΦen² pro vertex shadery. Tento krßtk² program je pak "spuÜt∞n" na ka₧d² vertex vaÜeho objektu. Vertex shader narozdφl od pixel shaderu lze nahradit softwarovou emulacφ, tzn. ₧e lze pou₧φt vertex shadery i na systΘmech se starÜφm ₧elezem. Tento systΘm budeme pou₧φvat, jen bude-li to pot°eba.
18.1.5. Matice
Dßle si n∞co povφme o maticφch a je t°eba abyste tuto Φßst dob°e pochopili. Pomocφ matic provßdφme v Direct3D transformace, tedy nejen ty, o kter²ch byla °eΦ p°ed chvilkou. Pozd∞ji se dozvφte, ₧e to nenφ jedin² zp∙sob transformace.
Matematickß vlo₧ka
P°edpoklßdßm, ₧e ka₧d² vφ, co je to vektor, ale pro ·plnost zde uvedu n∞kolik poznßmek z analytickΘ geometrie a z lineßrnφ algebry.
Vektor
Vektor je obecn∞ n-tice Φφsel nap°. vektor r = (r1, r2,
..., rn). My ale budeme pou₧φvat vektory 2-4 rozm∞rnΘ. Polohov²m
vektorem je popsßna poloha bodu v prostoru Φi v rovin∞. Nap°φklad u
normßlovΘho vektoru nßs zajφmß p°edevÜφm sm∞r a nikoliv koncov² bod (navφc
se v∞tÜinou pracuje s jednotkov²m vektorem, jeho₧ velikost je rovna 1).
Mimochodem velikost vektoru m∙₧eme spoΦφtat pomocφ nßsledujφcφho vzorce:
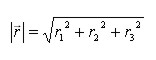
D∙kaz vztahu zde vynechßm. V praxi ale budeme moci pou₧φvat funkce D3DX knihovny, kterß je souΦßstφ SDK. Struktury 2-4 rozm∞rn²ch vektor∙ jsou tedy D3DXVECTOR2, D3DXVECTOR3 nebo D3DXVECTOR4. Funkce, kterΘ vracφ velikost vektor∙ se naz²vajφ D3DXVec2Length(), D3DXVec3Length() nebo D3DXVec4Length().
Matice
Matice je tedy op∞t n∞jakß uspo°ßdanß skupina Φφsel. Budeme v²hradn∞ pou₧φvat matice 4x4, kterou vidφte na dalÜφm obrßzku:
Nynφ si ukß₧eme, jak probφhß transformace pomocφ tΘto matice. Transformovat vektor znamenß vynßsobit ho touto maticφ:
P∙vodnφ vektor (x, y, z) transformujeme pomocφ matice M na Φßrkovan² vektor (x, y, z) nßsledovn∞:
Maticemi m∙₧ete provßd∞t posuvn² pohyb (translaci), otßΦiv² pohyb (rotaci) nebo zm∞nu m∞°φtka (scaling).
Nynφ si proberme jednotlivΘ transformace:
Translace
Pokud chceme bod v prostoru posunout, staΦφ ho vynßsobit nßsledujφcφ maticφ:
Kde Tx, Ty a Tz jsou relativnφ ·seky v prostoru, o kterΘ se bod posune. V knihovn∞ je op∞t funkce D3DXMatrixTranslation(), pomocφ kterΘ vytvo°φme p°φsluÜnou translaΦnφ matici.
Rotace
Rotovat lze objektem kolem vÜech t°φ os a pro ka₧dou z t∞chto rotacφ musφ b²t zvlßÜ¥ matice:
Kolem osy x, kde θ ·hel otoΦenφ v radißnech:
Kolem osy y:
Kolem osy z:
A op∞t je tu trojice funkcφ, kterΘ vytvo°φ p°φsluÜnΘ rotaΦnφ matice: D3DXMatrixRotationX(), D3DXMatrixRotationY() a D3DXMatrixRotationZ().
Zm∞na m∞°φtka - scaling
Scaling m∙₧e b²t bu∩ uniformnφ Φi nikoliv. Uniformnφ znamenß, ₧e zm∞na m∞°φtka je podle vÜech os ekvivalentnφ, ale m∙₧ete t∞leso protßhnout t°eba jen v jednom sm∞ru pomocφ neuniformnφho scalingu. Scaling provßdφme pomocφ nßsledujφcφ matice:
Kde sx, sy a sz jsou hodnoty, o kterΘ se t∞leso protßhne (smrÜtφ) ve sm∞rech jednotliv²ch os. Pokud je hodnota v∞tÜφ ne₧ 1, t∞leso se v tomto sm∞ru zv∞tÜuje, jeli hodnota menÜφ ne₧ 1, t∞leso se smrÜ¥uje. Zadßte-li nap°φklad hodnoty sx, sy rovno 1, docφlφte neuniformnφho scalingu ve sm∞ru osy z. I pro tuto transformaci existuje funkce D3DXMatrixScaling(), kterß vytvo°φ v²Üe uvedenou matici.
Sklßdßnφ matic
DalÜφ v²hodou matic je, ₧e m∙₧ete jednotlivΘ "efekty" slo₧it do jednΘ matice. Prost∞ je staΦφ mezi sebou vynßsobit a tφm spojφte efekty v nich ulo₧enΘ. Vynßsobφte-li nap°φklad matici translace a rotace, bod, kter² touto v²slednou maticφ transformujete se posune a otoΦφ se kolem jednΘ z os.
K nßsobenφ m∙₧ete vyu₧φt funkci D3DXMatrixMultiply(). U nßsobenφ matic je d∙le₧itΘ, ₧e zßle₧φ na po°adφ v jakΘm nßsobenφ provßdφte - neplatφ zde komutativnφ zßkon. Transformace se provßdφ zleva doprava, tak₧e nejprve se provede transformace uvedenß na prvnφm mφst∞. Nap°φklad:
C = R * T
C je slo₧enß matice, R je rotaΦnφ matice a T je translaΦnφ matice. Nejprve se tedy provede rotace a poslΘze translace.
A je tu op∞t konec dalÜφ lekce. Dnes jsme nakousli rozsßhlΘ tΘma Direct3D: nejprve jsme si pov∞d∞li n∞co architektu°e Direct3D, dßle jsem popsal prostor a elementßrnφ objekt - troj·helnφk, takΘ jsme se zab²vali zpracovßnφm vertex∙ a nakonec jsme probrali vÜechny mo₧nΘ transformace.
V p°φÜtφ lekci ji₧ vytvo°φme prvnφ Direct3D aplikaci. Zjistφte, ₧e zaΦßtky jsou podobnΘ jako v DirectDraw.
T∞Üφm se p°φÜt∞ nashledanou.