GravitaΦnφ pole Autor:TomßÜ Vostr² GravitaΦnφ pole - existuje kolem ka₧dΘho t∞lesa, projevuje se silov²m p∙sobenφm na jinß t∞lesa - gravitaΦnφ pole nßle₧φ Zemi, M∞sφci, Slunci - vlastnosti t∞les p°i vzßjemnΘm p∙sobenφ v gravitaΦnφm poli se naz²vß gravitaΦnφ interakce - sφly vzniklΘ mφrou p∙sobenφ jsou tzv. gravitaΦnφ sφly, fyzikßlnφ jev pak souhrnn∞ naz²vßme gravitace. Newton∙v gravitaΦnφ zßkon Zn∞nφ: Dva hmotnΘ body se navzßjem p°itahujφ stejn∞ velk²mi gravitaΦnφmi silami s navzßjem opaΦn²m sm∞rem. Velikost gravitaΦnφ sφly je pak p°φmo ·m∞rnß souΦinu hmotnostφ m1,m2 hmotn²ch bod∙, ale nep°φmo druhΘ mocnin∞ jejich vzdßlenosti r. - matematicky je tento zßkon vyjßd°en nßsledovn∞: Intenzita gravitaΦnφho pole - znaΦφ se K, jde o vektorovou veliΦinu - vyjad°uje silovΘ p∙sobenφ gravitaΦnφho pole v jeho Φßstech - platφ ₧e, intenzita gravitaΦnφho pole K je v urΦitΘm mφst∞ vyjßd°ena jako podφl gravitaΦnφ sφly Fg, p∙sobφcφ v danΘm mφst∞ na hmotn² bod a hmotnosti m tohoto t∞lesa - jednotkou pak je newton na kilogram (N.kg-1) - matematicky dßno: - velikost intenzity K v danΘm mist∞ gravitaΦnφho je zßvislß jen na hmotnosti M t∞lesa, vytvß°ejφcφ pole, zßrove≥ vÜak zßvisφ na vzdßlenosti r tohoto mφsta od st°edu danΘho t∞lesa. Intenzita gravitaΦnφho pole Zem∞ - velikost intenzity gravitaΦnφho pole Zem∞ v urΦitΘ v²Üce h nad Zemφ je vyjßd°en matematick²m vztahem: - homogennφ gravitaΦnφ pole = gravitaΦnφ pole, kterΘ mß ve vÜech mφstech stejnou intenzitu K GravitaΦnφ zrychlenφ - gravitaΦnφ sφla Fg ud∞lφ t∞lesu s hmotnostφ m zrychlenφ, kterΘ pak naz²vßme gravitaΦnφ zrychlenφ - znaΦφ se ag - platφ vztah: K = ag, z Φeho₧ vypl²vß, ₧e intenzita gravitaΦnφho pole v urΦitΘm mφst∞ pole je rovna zrychlenφ, ud∞lenΘmu v tomto bod∞ t∞lesu gravitaΦnφ silou. TφhovΘ zrychlenφ - projevuje se p∙sobenφm tφhovΘ sφly Fg, kdy se t∞leso voln∞ pohybuje ve vakuu se zrychlenφm g, takovΘmu zrychlenφ °φkßme gravitaΦnφ - sm∞r zrychlenφ je svisl² - prostoru nad Zemφ, kde se projevujφ ·Φinky tφhovΘ sφly oznaΦujeme pojmem tφhovΘ pole. Pohyby t∞les v homogennφm tφhovΘm poli Zem∞ - nejjednoduÜÜφm je voln² pßd - jde o pohyb rovnom∞rn∞ zrychlenφ s nulovou poΦßteΦnφ rychlostφ a s tφhov²m zrychlenφm g Vrh t∞lesa - jde o slo₧en² pohyb, tvo°φ ho pohyb rovnom∞rn² p°φmoΦar² a voln² pßd - svisl² vrh = pohyb rovnom∞rn∞ zpomalen² - velikost rychlosti v v Φase t, lze vyjßd°it nßsledujφcφm vztahem: v= v0-gt - pro okam₧itou v²Üku y t∞lesa v Φase t: Vodorovn² vrh - trajektoriφ je Φßst paraboly - zvolme si osy x a y, sou°adnice mφsta vrhu A jsou pak pro rychlost v mß sm∞r osy x, pak sou°adnice bodu B, ve kterΘm se t∞leso ocitne za Φas t lze popsat vztahem: - nejv∞tÜφ vzdßlenost od mφsta vrhu se oznaΦuje jako dΘlka vrhu, matematicky se zφskß vzorcem: èikm² vrh vzh∙ru - trajektorie = Φßst paraboly, kterß svφrß s vodorovnou rovinou tzv. elevaΦnφ ·hel - zvolme si op∞t sou°adnicovou soustavu, kde mφsto vrhu = A, sou°adnice a pak sou°adnice bodu B, co₧ je mφsto, kde se t∞leso objevφ za Φas t m∙₧eme vyjßd°it nßsledovn∞: - maximßlnφ dΘlka vrhu je p°i velikosti elevaΦnφho ·hlu 45o to vÜak platφ pouze pro vakuum. P°i st°elb∞ ve vzduchu se docφlφ maximßlnφ dΘlky vrhu p°i velikosti elevaΦnφho ·hlu 42o. Parabolickß trajektorie se deformuje a zφskßvß podobu balistickΘ k°ivky. Pohyby t∞les v centrßlnφm gravitaΦnφm poli Zem∞ - jsou takovΘ pohyby, jejich₧ trajektorie zasahujφ do mφst, ve kter²ch se ji₧ nemluvφ o homogennφm gravitaΦnφm poli Zem∞ - podΘl trajektorie se m∞nφ sm∞r i velikost intenzity gravitaΦnφho pole K, zßrove≥ s tφm takΘ gravitaΦnφ zrychlenφ ag sm∞°ujφcφ do gravitaΦnφho sm∞ru Zem∞ - pom∞rn∞ malß poΦßteΦnφ rychlost = trajektoriφ je Φßst elipsy - urΦitß hodnota poΦßteΦnφ rychlosti = kruhovß rychlost, trajektoriφ je kru₧nice (pohyb um∞l²ch dru₧ic kolem Zem∞) - platφ: Fd = Fg, vzorec pro kruhovΘ zrychlenφ: - 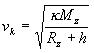hodnota ag = 9,81 m.s-1 a Rz = 6,37.106 zφskßme vk = 7,90 km.s-1, mluvφme o prvnφ kosmickΘ rychlosti, ob∞₧nß doba t∞lesa T = 84,4 min. - trajektorie = elipsa, apogeum - nejv∞tÜφ vzdßlenost od st°edu Zem∞, perigeum - nejmenÜφ vzdßlenost od st°edu Zem∞ - druhß kosmickß rychlost - vp = 11,2 km.s-1 Pohyby t∞les v centrßlnφm gravitaΦnφm poli Slunce Prvnφ Kepler∙v zßkon: Planety se pohybujφ kolem Slunce po elipsßch, kterΘ jsou jen mßlo odliÜnΘ od kru₧nic, v jejich₧ spoleΦnΘm ohnisku se nachßzφ Slunce. Druh² Kepler∙v zßkon: Obsahy ploch opsan²ch provodiΦem planety b∞hem jednotky Φasu jsou konstantnφ. - nejkratÜφ pr∙vodiΦ je v perihΘliu (p°φslunφ), nejdelÜφ v afΘliu (odslunφ) T°etφ Kepler∙v zßkon: Pom∞r druh²ch mocnin ob∞₧n²ch dob dvou planet je roven pom∞ru t°etφch mocnin hlavnφch poloos jejich trajektoriφ. - tento zßkon lze matematicky vyjßd°it: - st°ednφ vzdßlenost planet od Slunce = astronomickß jednotka AU = r = 149,6.106 km.