 |
|
ZČU - Fakulta pedagogická
Ukázka testu z matematiky
-
V R řešte rovnici:

-
V rovině jsou dány body:

Určete:
a) velikost vnitřního úhlu při vrcholu B v trojúhelníku ABC,
b) obsah trojúhelníku ABC
-
Do koule o poloměru r je vepsán kvádr, jehož rozměry jsou v poměru 2:3:6. Určete, v jakém poměru jsou objemy těchto těles.
-
Dokažte, že všechny hodnoty výrazu
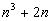 , kde n je přirozené číslo, jsou dělitelné třemi. , kde n je přirozené číslo, jsou dělitelné třemi.
-
Dřevěnou krychli o hraně velikosti 5 cm, která je natřena modře, rozřežeme na jednotkové krychle ( o hraně 1 cm). Určete pravděpodobnost, že při namátkovém výběru z nich vybereme:
a) krychli se dvěma modrými stěnami,
b) krychli s jednou nebo dvěma modrými stěnami.
-
Jestliže výrazy
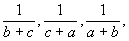 v nichž čísla a, b, c, nabývají přípustných hodnot, tvoří tři po sobě jdoucí členy aritmetické posloupnosti, pak také čísla v nichž čísla a, b, c, nabývají přípustných hodnot, tvoří tři po sobě jdoucí členy aritmetické posloupnosti, pak také čísla 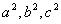 tvoří tři po sobě jdoucí členy aritmetické posloupnosti. Dokažte! tvoří tři po sobě jdoucí členy aritmetické posloupnosti. Dokažte!
Výsledky
-
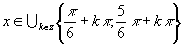
-
a)
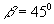
b)P=15
-
kvádr: úhlopříčka
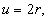 rozměry : rozměry : 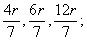 V koule: V koule: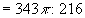 V kvádru. V kvádru.
-
Postupně pro
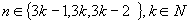 dokážeme, že výraz dokážeme, že výraz  je násobkem tří. je násobkem tří.
-
z celkového počtu 125 jednotkových krychlí má: 8 krychlí 3 modré stěny, 36 krychlí 2 modré stěny, 54 krychlí 1 modrou stěnu a 27 krychlí nemá žádnou modrou stěnu

-
a)z rovnosti
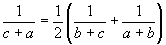 dostaneme dostaneme 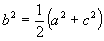
|
|
|
|
 |