 |
|
JČU - Fakulta pegagická
Test z matematiky
- Určete všechna reálná čísla x, pro něž platí
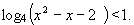
- Jsou dány body A[1,2], B[3,4], V[2,-1]. Určete bod C tak, aby byl bod V průsečíkem výšek v trojúhelníku ABC.
- Muž 1,8 m vysoký kráčí po nábřeží přímo k majáku. Stín tohoto muže od světla majáku je zpočátku 5,4 m dlouhý. Když muž popošel k majáku o 90 cm, zkrátil se jeho stín o 3 m. Jak vysoký je maják a jak daleko stál původně muž od majáku?
- Zobrazte v Gaussově rovině všechna komplexní čísla z, pro něž platí
 a zapište je v algebraickém a goniometrickém tvaru. a zapište je v algebraickém a goniometrickém tvaru.
- Vypočtěte všechna reálná čísla x, pro něž platí
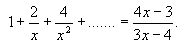
Výsledky:

- rovnice přímka
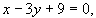 výšky výšky 
- výška majáku v = 55,8 m; vzdálenost muže od majáku 167,4 m
- sjednocení 2 polopřímek:
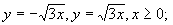 komplexní čísla, jejichž obrazy leží na polopřímce komplexní čísla, jejichž obrazy leží na polopřímce 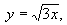 lze zapsat ve tvaru lze zapsat ve tvaru  resp. resp. 
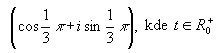
- 5. kvocient geometrické řady
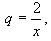 podmínka konvergence podmínka konvergence 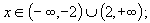 ; součet řady ; součet řady 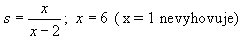 ( x = 1 nevyhovuje) ( x = 1 nevyhovuje)
|
|
|
|
 |