Fraktßlnφ geometrie a poΦφtaΦovß grafika - principy a algoritmy



Zßklady fraktßlnφ geometrie polo₧il p°ed vφce ne₧ t°iceti lety matematik B. B. Mandelbrot. On sßm ji oznaΦil za morfologii amorfnφho. Nezßvisle na nφ vznikla zhruba v tΘ₧e dob∞ teorie tzv. deterministickΘho chaosu. V podstat∞ se nezßvisle na r∙zn²ch mφstech vytvo°ilo novΘ tΘma ve v∞d∞: hledßnφ °ßdu v chaosu.

Klasickß euklidovskß geometrie se zab²vß studiem ideßlnφch pravideln²ch ·tvar∙ jako Φtverce, kru₧nice, pravidelnΘ mnoho·helnφky a mnohost∞ny. Naproti tomu fraktßlnφ geometrie studuje tvary tak ΦlenitΘ jako t°eba hory, pob°e₧φ, mraky, elektrickΘ v²boje, stromy, ÜpinavΘ skvrny a podobn∞. Odtud plyne jejφ praktickΘ vyu₧itφ v poΦφtaΦovΘ grafice a simulaci.

Budeme studovat vlastn∞ limity posloupnostφ mno₧in, kterΘ se vyznaΦujφ opakovßnφm tΘho₧ vzoru ve stßle menÜφm m∞°φtku. Vlastnost b²t invariantnφ v∙Φi zm∞n∞ m∞°φtka nazval Mandelbrot sob∞podobnost (self-similarity). K "m∞°enφ" takov²ch ·tvar∙ ji₧ nelze pou₧φt prost°edky klasickΘ geometrie. Proto se jako mφra Φlenitosti definuje tzv. Hausdorfova dimenze. Jejφ definice je slo₧itß, ale pro dosti velkou t°φdu sob∞podobn²ch mno₧in lze Hausdorfovu dimenzi spoΦφtat podle jednoduchΘho vzorce. V p°φpad∞, ₧e nßmi zkouman² objekt obsahuje n kopiφ sebe sama zmenÜen²ch na jednu k-tinu je Hausdorfova dimenze rovna log(n) / log(k). LΘpe to ukß₧eme na p°φkladu.

Jednφm z nejjednoduÜÜφch fraktßlnφch ·tvar∙ je Cantorovo diskontinuum. ZaΦneme s ·seΦkou libovoln∞ zvolenΘ dΘlky. Tu rozd∞lφme na t°etiny a prost°ednφ Φßst sma₧eme. Zφskßme tak dv∞ ·seΦky, s nimi₧ postup opakujeme. Kdybychom totΘ₧ opakovali a₧ donekoneΦna, zφskali bychom mno₧inu nekoneΦn∞ mnoha bod∙, jejich₧ celkovß dΘlka by byla 0. To je Cantorovo diskontinuum. VÜimn∞me si nynφ, ₧e takovß mno₧ina obsahuje dv∞ kopie sebe sama zmenÜenΘ na t°etinu. Hausdorfova dimenze Cantorova diskontinua je tedy log 2 / log 3 = 0.6309...



Prvnφch Üest aproximacφ Cantorova diskontinua

Pojem Hausdorfovy dimenze pou₧il Mandelbrot pro exaktnφ definici sob∞podobnΘ mno₧iny, kterou nazval fraktßl. Je to takovß podmno₧ina euklidovskΘho prostoru, pro ni₧ je Haudorfova dimenze ost°e v∞tÜφ ne₧ dimenze topologickß (viz nφ₧e). HladkΘ k°ivky majφ Hausdorfovu dimenzi rovnou 1, avÜak s rostoucφ Φlenitostφ tato dimenze roste. Dokonce existujφ k°ivky, jejich₧ Hausdorfova dimenze je rovna 2. Podobn∞ dvojrozm∞rnΘ ·tvary s Hausdorfovou dimenzφ v∞tÜφ ne₧ 2 jsou fraktßly.

Sob∞podobnΘ obrazce se dajφ velice dob°e aproximovat poΦφtaΦem. Opakovßnφ tΘho₧ vzoru se p°irozen∞ realizuje volßnφm tΘho₧ podprogramu se stßle zmenÜujφcφmi se parametry. Pokud do t∞chto algoritm∙ zavedeme nßhodn² prvek dostaneme takzvanΘ statisticky sob∞podobnΘ fraktßly. Nap°φklad v Cantorov∞ diskontinuu nebudeme ·seΦky d∞lit na t°etiny, ale zvolφme nßhodn∞ dva body. Pomocφ takov²chto algoritm∙ se dajφ velmi dob°e simulovat mnohΘ p°φrodnφ ·tvary. Krßsa statisticky sob∞podobn²ch fraktßl∙ spoΦφvß v k°ehkΘ harmonii mezi pravidelnostφ a nahodilostφ. Stejn∞ jako krßsa p°φrody. V lese nepanuje chaos, p°esto₧e je ka₧d² strom jedineΦn². Proto se nßm les zdß krßsn∞jÜφ ne₧ sφdliÜt∞ se svojφ um∞lou pravidelnostφ i ne₧ smetiÜt∞, kterΘ je ·pln∞ chaotickΘ.

P°i studiu mno₧in invariantnφch v∙Φi nelineßrnφm transformacφm objevil Mandelbrot nep°ebernΘ mno₧stvφ krßsn²ch a zajφmav²ch fraktßl∙. NejjednoduÜÜφ t°φdou jsou Juliovy mno₧iny, kterΘ si nynφ blφ₧e popφÜeme. NejjednoduÜÜφ nelineßrnφ racionßlnφ komplexnφ funkce je kvadratick² polynom fc (z) = z 2+ c, kde c je komplexnφ parametr. Juliova mno₧ina tΘto funkce je hranice mno₧iny t∞ch z, pro kterß je posloupnost { fc(z), fc fc(z)=fc2, ... }, vytvo°enß postupn²m iterovßnφm tΘto funkce, omezenß. Sv∞t tvar∙ Juliov²ch mno₧in je neoΦekßvan∞ bohat². S v²jimkou c=0 (jednotkovß kru₧nice) a c=-2 (reßln² interval <-2, 2>) jsou Juliovy mno₧iny sob∞podobnΘ fraktßlnφ mno₧iny nejr∙zn∞jÜφch tvar∙. Pokud bod∙m obrazovky p°i°adφme komplexnφ Φφsla analogicky jako v Gaussov∞ rovin∞, m∙₧eme urΦit barvu podle rychlosti divergence iteracφ. Tak zφskßme p°ekvapiv∞ estetickΘ obrazy, kterΘ je mo₧nΘ dßle vyu₧φt v poΦφtaΦovΘ grafice.


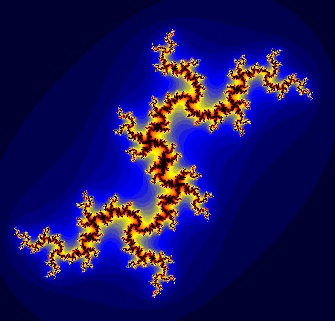
Takhle vypadß Juliova mno₧ina pro c = -0.76i
DalÜφ zajφmavΘ tvary Juliov²ch mno₧in na vßs Φekajφ tady.


KlφΦem ke klasifikaci chovßnφ funkcφ fc (z) = z 2 + c v zßvislosti na parametru c je tzv. Mandelbrotova mno₧ina. Je to mno₧ina takov²ch c, pro kterß je Juliova mno₧ina funkce fc (z) souvislß. P. Fatou a G. Julia ukßzali, ₧e mno₧ina je souvislß prßv∞ kdy₧ je posloupnost { c, c2+ c, (c2+ c)2+ c, ... } omezenß. Topologickß dimenze Juliov²ch mno₧in zßvisφ na poloze parametru c vzhledem k Mandelbrotov∞ mno₧in∞ M: Je-li c uvnit° M, pak je topologickß dimenze rovna 2, je-li c na hranici M, pak je dimenze 1 a je-li c mimo M je topologickß dimenze rovna 0. Dlu₧no dodat, co je to topologickß dimenze. Tenhle exaktnφ pojem de facto odpovφdß intuitivnφmu pojmu rozm∞r. K°ivky jsou jednorozm∞rnΘ, ploÜnΘ ·tvary dvojrozm∞rnΘ, prostorovΘ trojrozm∞rnΘ apod. Mno₧iny bod∙ rozmφst∞n²ch nesouvisle majφ topologickou dimenzi 0.


Mandelbrotova mno₧ina je z°ejm∞ nejznßm∞jÜφ fraktßlnφ ·tvar.


Klepnutφm sem si m∙₧ete stßhnout moje zdrojßky v Borland Pascalu pro DOS. Jsou to dva programy, kterΘ generujφ Juliovy mno₧iny a Mandelbrotovu mno₧inu. Unita rat.tpu slou₧φ k zßkladnφmu ovlßdßnφ myÜi. Jejφ zdrojßk mi zniΦily Windows, ale pou₧itφ t∞ch rutin je intuitivnφ. Komentß°e pφÜu v angliΦtin∞, doufßm, ₧e to nikomu nevadφ. P°ipojil jsem i podrobnou dokumentaci v ΦeÜtin∞ jako .txt bez diakritiky.

Pro obecnou komplexnφ racionßlnφ funkci majφ vÜechny oblasti p°ita₧livosti spoleΦnou hranici, na nφ₧ je dynamika chaotickß. P∞kn²m p°φkladem takovΘ funkce je f(z) = ( 2z 3 + 1) / 3z 2, pomocφ nφ₧ lze takzvanou Newtonovou iteraΦnφ metodou najφt ko°eny rovnice z 3 - 1 = 0. Tento dynamick² systΘm mß t°i jednobodovΘ atraktory (ko°eny zmφn∞nΘ rovnice). V oblasti p°ita₧livosti ka₧dΘho z t∞chto t°φ atraktor∙ je Newtonova metoda ·Φinnß, nebo¥ vyjdeme-li z libovolnΘho bodu oblasti, dostaneme postupn²m iterovßnφm funkce ( 2z 3 + 1) / 3z 2 posloupnost konvergujφcφ k p°φsluÜnΘmu ko°enu rovnice. Tyto t°i oblasti majφ spoleΦnou hranici, Juliovu mno₧inu funkce ( 2z 3 + 1) / 3z 2, na nφ₧ je Newtonova metoda ne·Φinnß. Tato hranice je zajφmav∞ Φlenitß fraktßlnφ mno₧ina s chaotickou dynamikou.


Newtonova metoda °eÜenφ rovnice z 3 - 1 = 0.


T°i oblasti p°ita₧livosti jsou barevn∞ rozliÜeny, jasnost barvy naznaΦuje rychlost konvergence. Op∞t dßvßm k dispozici sv∙j zdrojov² text v Pascalu. Jako shrnutφ nßsleduje nßvod, jak si vytvo°it vlastnφ fraktßl - Juliovu mno₧inu.

Vezm∞te jakoukoli racionßlnφ komplexnφ funkci, kterß vßs napadne. Iterovßnφ se provßdφ nßsledovn∞: vyjd∞te z n∞jakΘho komplexnφho Φφsla, dosa∩te do vaÜφ funkce a v²sledek op∞t pou₧ijte jako vstup. Zjist∞te jakoukoli metodou (t°eba i pokus-omyl) n∞kter² z atraktor∙ posloupnosti vzniklΘ iterovßnφm. Pak u₧ staΦφ m∞°it, jak rychle posloupnost konverguje k tomuto atraktoru (diverguje). Pokud je atraktor nekoneΦno, obvykle staΦφ m∞°it po kolika iteracφch p°esßhne Φlen posloupnosti urΦitou absolutnφ hodnotu. Pokud je jednobodov², staΦφ si zvolit konstantu epsilon a zjiÜ¥ovat, po kolika iteracφch se p°iblφ₧φme na epsilonovou vzdßlenost (p°esnost). Ka₧dΘmu pixelu p°irozen²m zp∙sobem p°i°adφte komplexnφ Φφslo (Gaussova rovina). To je v²chozφ bod pro iterovßnφ. Barva tohoto pixelu bude odpovφdat zjiÜt∞nΘ rychlosti konvergence.

Pokud vßs fraktßlnφ grafika zajφmß a chcete vid∞t na vlastnφ oΦi, co dokß₧e, podφvejte se na tohle!
Mßte-li dojem, ₧e v textu chybφ n∞kterΘ definice, mßte pravdu. Na po₧ßdßnφ vßm je dodßm, ale pro rßmec tohoto Φlßnku se mi zdßly p°φliÜ slo₧itΘ.
P°i programovßnφ se vßm bude hodit unita mode101h.pas.

Linx: The Mandelbrot Set and Julia Sets, Jemn² ·vod do fraktßl∙
Zdrojem informacφ mi byl p°edevÜφm Φasopis Pokroky matematiky, fyziky a astronomie, roΦnφk 34 (1989), Φφslo 5.
P°ipomφnky posφlejte autorovi strßnky. M∙₧ete se vrßtit zp∞t na homepage anebo tam, odkud jste p°iÜli.