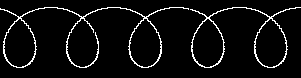e╢li czyta│e╢ m≤j tekst o fraktalach i zagadnienie Ciebie zainteresowa│o, to warto tak┐e przeczytaµ o zagadnieniu bardzo bliskim poprzedniemu, gdy┐ dotycz▒cego tak┐e zabawy z krzywymi, tym razem cykloidami. Nie przedstawiam tu gotowego programu, a jedynie kod ╝r≤d│owy do Turbo Pascala, gdy┐ pe│ni przyjemno╢ci mo┐na doznaµ tylko przez w│asne modyfikacje algorytmu:-)
Na pocz▒tek bΩdzie Ci potrzebny algorytm rysowania okrΩgu. Odbywa siΩ to przez stawianie na ekranie punkt≤w o odpowiednio wyliczonych wsp≤│rzΩdnych. Wsp≤│rzΩdne aktualnie stawianego punktu wylicza siΩ z wzoru:
x=xs+r*sin(k)
y=ys+r*cos(k)
Je╢li czyta│e╢ o fraktalach, te wzory nie s▒ Ci obce, ale dla nowicjuszy kilka wyja╢nie±. xs oraz ys to wsp≤│rzΩdne ╢rodka okrΩgu, r - promie± okrΩgu. Wyja╢niµ nale┐y jeszcze zmienn▒ k. Jest to liczba rzeczywista zwiΩkszana w ka┐dej pΩtli o pewn▒ ma│▒ warto╢µ. Warto╢µ tΩ nale┐y dobraµ eksperymentalnie, przyjmijmy, ┐e zmieniamy k o 0.001 w ka┐dej pΩtli tak d│ugo, a┐ k=2*pi (w≤wczas zostanie narysowany ca│y okr▒g). Je╢li w praktyce bΩdzie on narysowany liczb▒ przerywan▒, to w ka┐dej pΩtli nale┐y zwiΩkszaµ k o mniejsz▒ warto╢µ.
W celu lepszego zrozumienia przetestuj nastΩpuj▒cy programik:
uses graph;
var
vga,vgahi: integer;
k:real;
begin
initgraph(vga,vgahi,'c:\bp\bgi');
k:=0;
repeat
putpixel(320+round(100*sin(k)),240+round(100*cos(k)),15);
k:=k+0.001;
until k=2*pi;
readln;
end.
Je╢li wszystko posz│o w porz▒dku, program wyrysowywa│ okr▒g o promieniu 100 pikseli w ╢rodku ekranu. Dla lepszego zrozumienia algorytmu zastan≤w siΩ, jaki powstanie rysunek, gdy warunek zako±czenia pΩtli zmienisz na k=pi. Spr≤buj nastΩpnie uruchomiµ program z tak▒ zmian▒. Czy rezultat jest taki, jak oczekiwa│e╢?
Do nastΩpnych pr≤b trzeba bΩdzie zmniejszyµ promie± rysowanego okrΩgu i zmieniµ warunek ko±czenia pΩtli na keypressed=true (zadeklaruj modu│ CRT). NastΩpnie zmie± algorytm tak, aby ╢rodek okrΩgu by│ lekko przesuwany w lewo, od warto╢ci 640, w co setnej pΩtli. W≤wczas na ekranie wy╢lietli siΩ taki "szlaczek":
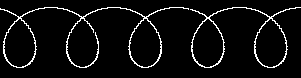
Teraz pora ciekawiej wykorzystaµ nasz efekt. W kolejnym programie nie bΩdziemy przesuwaµ ╢rodek nie po prostej, ale po okrΩgu(!). Zauwa┐my, ┐e wsp≤│rzΩdne 320 i 240 nale┐y pozostawiµ w algorytmnie, aby obraz by│ w miarΩ wy╢rodkowany. Je╢li procedurΩ putpixel z poprzedniego programu zmodyfikujesz tak:
putpixel(320+round(150*sin(k))+round(70*sin(k*10)),240+round(150*cos(k))+round(70*cos(k*10)),15);
to otrzymasz tak▒ figurΩ:
Wystarczy dalej modyfikowaµ w podobny spos≤b nasz▒ procedurΩ putpixel, aby uzyskiwaµ jeszcze ciekawsze obrazy. Je╢li post▒piµ analogicznie jak poprzednio i do pierwszego parametru dodaµ "round(20*sin(k*100))", a do drugiego "round(20*cos(k*100))", aby ╢rodek najmniejszego rysowanego okrΩgu sam siΩ przemieszcza│ po innym, wiΩkszym okrΩgu (itd.), to da to taki efekt:
ZachΩcam do dalszej manipulacji, tym razem ju┐ we w│asnym zakresie, na parametrach funkcji. Je╢li uda Ci siΩ zrobiµ co╢ ciekawego, z pewno╢ci▒ chΩtnie umieszczΩ to na stronie. Powodzenia!!!
