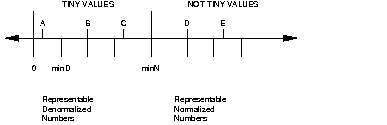
Figure 5-1 shows pictorially the IEEE definition of floating-point numbers. Only the positive side of the real number line is shown, but there is a corresponding negative side also. The tick marks under the real number line denote example values that can be precisely represented by a single or double precision binary number. The smallest representable value larger than zero is minD, a denormalized number. The smallest normalized number is minN. The region between zero and just less than minN contains tiny values. Larger values starting with minN are not tiny.

Figure 5-1 : Floating Point Numbers The different cases that must be considered are represented by the values A-E. According to the IEEE Standard, the behavior of an operation that produces these result values is defined as shown in Table 5-1.
The flags U and I abbreviate Underflow and Inexact, respectively. The function rnd() rounds the operand to the nearest representable floating point number based on the current rounding mode, which can be round-to-zero, round-to-nearest, round-to-plus-infinity, and round-to-minus-infinity. For example, rnd(A) is either zero or minD. A trap occurs if a flag is set and the corresponding enable is on. For example, if an operation sets I=1 and EnableI=1, then a trap should occur. Note that there is a special case for representable tiny values: the setting of the U flag depends on the setting of its enable.
Supporting denormalized numbers in hardware is undesirable because many high performance hardware algorithms are designed to work only with normalized numbers, and so a special case using additional hardware and usually additional execution time is needed to handle denormalized numbers. This special case hardware increases the complexity of the floating-point unit and slows down the main data path for normalized numbers, but is only rarely used by a few applications. Therefore most processor designers have generally deemed it not cost effective to support computations using denormalized numbers in hardware. To date no implementation of the MIPS architecture supports denormalized number in hardware.
Computations using denormalized numbers can also be supported by software emulation. Whenever a floating-point operation detects that it is about to either generate a denormalized result or begin calculating using a denormalized operand, it can abort the operation and trap to the operating system. A routine in the kernel, called softfp, emulates the computation using an algorithm that works correctly for denormalized numbers and deposits the result in the destination register. The operating system then resumes the application program, which is completely unaware that a floating-point operation has been emulated in software rather than executed in hardware. Emulation via softfp is the normal execution environment on all IRIX platforms today.
The problem with the software emulation approach is two-fold. Firstly, emulation is slow. Computations using denormalized operands frequently generate denormalized results. So, once an application program creates a denormalized intermediate value, the execution speed of the application drastically slows down as it propagates more and more denormalized intermediate results by software emulation. If the application truly requires representation of denormalized numbers in order to perform correctly, then the slowdown is worthwhile. But in many cases the application also performs correctly if all the denormalized intermediate results were rounded to zero. For these applications software emulation of denormalized computations is just a waste of time.
The second problem with software emulation is that it demands precise floating-point exceptions. In order for softfp to substitute the result of an arbitrary floating-point instruction, the hardware must be capable of aborting an already-executing floating-point instruction based on the value of the input operand or result, aborting any subsequent floating-point instruction that may already be in progress, and trapping to the operating system in such a way that the program can be resumed. Providing precise exceptions on floating-point operations is always difficult since they take multiple cycles to execute and should be overlapped with other operations. It becomes much more difficult when, to achieve higher performance, operations are executed in a different order than that specified in the program. In this case instructions logically after a floating-point operation that needs to be emulated may have already completed execution! While there are known techniques to allow softfp to emulate the denormalized operation, all these techniques require considerable additional hardware.