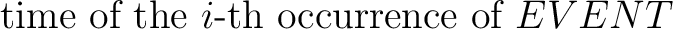) : {time = 0}P{
}
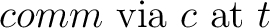In [51,50], an assertional style of reasoning about real-time systems is introduced, based on classical Hoare triples {q}P{r}. P is a program, and q and r are first order predicates [49]. Hoare triples can only express partial correctness (properties that hold if the program terminates). This however is not suitable for real-time programs which must deal with non-terminating processes and intensive interaction with the environment.
Therefore Hoare triples are extended with a third assertion C called a commitment. This leads to formulas of the form C : {q}P{r}. The commitment expresses the communication interface of the program P (part of the controller) with the environment (the plant or other parts of the controller). The commitment must be satisfied by terminating and non-terminating computations. Communication between processes is by message passing only (there are no shared variables), so C contains no program variables. The special time variable time is allowed in the commitment.
The specification asserting that P does not perform any communication on channel c is written
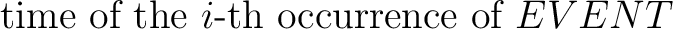) : {time = 0}P{}
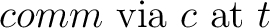A sound and relatively complete compositional proof system is provided for Occam style programs. The first extension of Hoare style reasoning from sequential to qualitative (non real-time) concurrent reasoning is provided in [113], but the proof system required the presence of all the code and hence was not compositional. To aid in the development of the proof system, a denotational semantics for Occam is developed. The execution model is based on maximal parallelism and synchronous message passing.
[50] compares MTL (metric temporal logic) and the assertional Hoare style proof systems. In general MTL allows for more concise real-time specifications than the more verbose assertional style. The assertional style of reasoning is more suitable for detailed reasoning about sequential program fragments. A combination of both styles of reasoning is recommended. Use concise MTL formulas for top level specifications and the initial design outline. Use the assertional style to perform detailed verification of sequential components. In both cases, compositional proofs of correctness are complex even for simple examples.