Untimed Process Algebras have been extended with timing constructs in several
ways including (in alphabetical order):
- ACPρ (Real-Time ACP) [8]. A dense time domain is used.
- ATP (Algebra of Timed Processes) [97].
- CCSR (Calculus of Communication Shared Resources based
on CCS) [32,33]. This algebra also provides a proof system for
dealing with priority based access to scarce resources.
- TCSP (Timed CSP) [126,127,132,128]. A dense time domain is
used.
- TCCS (Temporal CCS) [93]. A complete set of axioms is presented
for discrete time domains, but the semantics can be given as either discrete
or dense.
- TCCS (Timed CCS) [144]. Discrete or dense time domains can be
used.
- TPCCS (Timed Probabilistic CCS) [37]. TPCCS was already
discussed in the context of branching time temporal logic in the previous
section. A discrete time domain is used.
- TPL (Temporal Process Language) [45]. A discrete time domain is
used.
- U-LOTOS (Urgent LOTOS) [14]. Discrete or dense time domains can
be used.
We mention a few examples illustrating syntactic extensions for timed
behaviour and then describe the general principles involved.
In TCSP, the CSP syntax is enriched with the additional process WAIT d,
where d is a non-negative unit of time. The wait process terminates
successfully after d units of time. All events recorded by processes
relate to a conceptual global clock, and a process can only engage in a finite
number of events in a bounded period of time.
There is a constant delay δ associated with each action. Consider a
user interface of a vending machine VM. The insertion of a coin is modelled
by the action coin and a time tdrop is the time allowed for the coin
to drop before the event button is made available. The user then
presses the button and the machine then offers a drink coke after a
short delay tcoke. If the operator ``;'' stands for sequential
composition of processes (i.e. P;Q means do P then do Q) then the timed
behaviour of the vending machine can be specified as [21]
| VM |
= |
coin → WAIT(tdrop - δ); |
|
| |
|
button → WAIT(tcoke - δ); |
|
| |
|
coke → WAIT(treset - δ);VM |
|
The vending machine presents the user with no choice of product, so the
button is an unnecessary feature of the interface. The hiding operator
VM\button may be used to conceal the button event from the user.
Hidden events occur as soon as they become available so we obtain using the
algebraic rules
| VM\button |
= |
coin → WAIT(tdrop + tcoke - δ); |
|
| |
|
coke → WAIT(treset - δ);VMS |
|
The delays before and after the button event are unaffected by the
hiding operator.
In TCCS (temporal CCS), the construct (t).P denotes a
process that will evolve into process P after exactly t units of time.
δ.P denotes the process that is willing to wait any amount of time
before behaving like P.
As an example, consider the alternating bit protocol ABP. The process ABP is
the parallel composition of the sender, the receiver and the medium. Internal
events (such as the acknowledgment signal between the medium and the sender)
are hidden or projected out.
In the internal behaviour of the sender, r is the time that the sender will
wait after sending a message before assuming the message has been lost and
retransmitting.
The specification S that ABP must satisfy is
S = δ.send.(d ).receive.(d ).S
i.e. S is a process that after some time sends a message, followed by a
transmission delay of d clock units. The transmission delay is the time
that it takes to transmit the message and receive an acknowledgment. Once the
message is received and acknowledged (this also takes d clock units), the
same behaviour is then repeated. The protocol is verified to be correct by
showing that if r > 2d then
ABP = S
The equality is interpreted in a labelled transition graph semantics. It means
that the graph of ABP is the same as that of S, modulo the occurrence of
any number of internally hidden transitions.
In [32,33], an extended version of CCS called CCSR is presented.
CCSR deals with timing properties as well as resource sharing based on a
priority semantics. Most real-time formalisms capture delays due to
synchronization. Resource specific details are abstracted out by assuming
idealistic operating environments. The problem with this abstraction is
that true parallelism may take place only at the system level where a group of
shared resources is executed simultaneously. Each resource, however, is
inherently sequential in nature. A resource can only execute a single action
at one point in time. This constraint leads naturally to an interleaving
notion of concurrency. On the other hand, scheduling algorithms
ignore the effect of process synchronization except for simple precedence
relations between processes.
The computation model of CCSR treats synchronization and scheduling. It
is resource based in that multiple resources execute synchronously, while
processes assigned to the same resource are interleaved according to their
priorities. CCSR possesses a prioritized equivalence for terms, based on strong
bisimilarity. An equational proof system is provided for syntactic manipulation
of terms based on resource configuration and priority ordering.
In [98], an overview of the above timed process algebras (TPAs) is
presented as well as a unifying framework for treating them. The authors of
[98] point out that most TPAs implicitly adopt the following view
concerning their operation:
- A timed system is the composition of cooperating sequential components
or processes. Each component has (semantically) a time variable as part
of its state defined on an appropriate domain D with binary operation +
(addition on nonnegative numbers). A component modifies its state
either by executing some atomic action (atomic actions take no time) or by
increasing its time variable (letting time progress).
- The time variable increases synchronously in all processes only if all
components accept to do so. (In some TPAs this results in the counterintuitive
notion that time stops).
- An execution sequence takes place in two phases. In phase 1,
components may execute a finite though arbitrarily long sequence of
actions either independently or in cooperation with each other. In phase 2,
components coordinate to let time progress by some finite (or infinite) amount.
An untimed process algebra is a quadruple
UPA = (O, A, R,∼) where O is a
set of operators defining the syntax of the language. L is a set of
transition labels (actions). R is a set of rules defining the operational
semantics or models, associating with each term of the language a transition
system. The relation ∼ is a behavioural equivalence (e.g. bisimulation)
defined over the models.
A labelled transition system (whose states are process expressions) is the main
computational model considered for the sake of comparing the various algebras.
P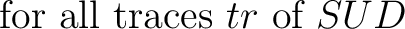 Q means the process P may perform the atomic and
timeless action a and then it behaves like Q. The transition
P
Q means the process P may perform the atomic and
timeless action a and then it behaves like Q. The transition
P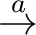 Q means that the process P may idle for d time
units after which it behaves like Q. A time domain is a commutative monoid
(D, + , 0). As D is usually infinite, models of processes are generally
infinitely branching transition systems.
Q means that the process P may idle for d time
units after which it behaves like Q. A time domain is a commutative monoid
(D, + , 0). As D is usually infinite, models of processes are generally
infinitely branching transition systems.
A timed process algebra is obtained from the untimed algebra
(O, A, R,∼)
by adding a set O' of time constraining operations. The timed process
algebra is then defined as
TPA = (O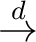 O', A, R',∼'). It must then be
decided how to obtain the operational semantic rules R' and the strong
equivalence ∼' with respect to the labelled transition system.
O', A, R',∼'). It must then be
decided how to obtain the operational semantic rules R' and the strong
equivalence ∼' with respect to the labelled transition system.
The two main constraints that must be satisfied are:
- Semantics Conservation.
- The untimed process and its timed equivalent
should have the same behaviour as long as we observe execution actions only.
This means that the untimed rules R remain valid in the corresponding TPA,
as far as they are applied on terms of the UPA.
- Isomorphism.
- For any terms P, Q of UPA, the equivalence P∼Q
holds iff P∼'Q. This requirement guarantees that any theoretical
development in UPA remains valid in TPA and conversely.
See [98] for a further discussion of how and to what extent these
constraints are satisfied in the various timed process algebras.
An important issue that arises is the finite variability property (or
non-Zeno behaviour) of the algebras. TCSP is the only algebra for which all
processes satisfy the finite variability property, namely, that a process can
only perform a finite number of actions in a finite time interval. A process
that has Zeno behaviours may be unrealizable. In TCSP, non-Zeno behaviour is
achieved by enforcing a system delay between two actions of a sequential
process. Thus the isomorphism requirement is not satisfied, and hence not
all laws of CSP are valid in TCSP. The assumption of a system
delay seems to be the only solution that ensures finite variability, but yields
instead a complicated theory which also destroys the abstractness of time
[98].
In algebras such as TCCS, U-LOTOS and
ACPρ there exist processes
whose models can block the progress of time. For timed systems it is
natural to demand that a terminated process does not block time; but then
a distinction must be made between termination and deadlock. The designers of
algebras that block time admit that such time-locks are counterintuitive.
However, they claim that time-locks can detect certain types of timing
inconsistencies and unrealizable specifications.
In summary, verifying that a timed process P satisfies a specification S
depends on whether a dual language framework is used or a single language
framework.
- In a dual language framework the specification S is a formula in a
high level logical language (e.g. S is a predicate over behaviours or
a temporal logic formula). The process P is an expression of an algebraic
process construction language. A proof system is provided in which there is a
rule relating each operator of the algebra to a predicate representing its
satisfying behaviours. A formal derivation that
P
 S can
then be constructed. This is the main method used for verification in TCSP.
The TCSP proof system has been used to prove the correctness of control
software for aircraft engines, of realistic telephone switching networks and
of a local area network protocol [128]. In TCSP there is also a method of
verification called timewise refinement. There is a hierarchy of
theories from the most abstract untimed theories to the most detailed timed
theories. Some specifications may be decomposed into a functional part and a
timed part. The functional part of the specification is checked more simply in
the untimed model, by using correctness-preserving migration between models in
the hierarchy. Only the timing part of the specification need be checked in
the more complex timed model.
S can
then be constructed. This is the main method used for verification in TCSP.
The TCSP proof system has been used to prove the correctness of control
software for aircraft engines, of realistic telephone switching networks and
of a local area network protocol [128]. In TCSP there is also a method of
verification called timewise refinement. There is a hierarchy of
theories from the most abstract untimed theories to the most detailed timed
theories. Some specifications may be decomposed into a functional part and a
timed part. The functional part of the specification is checked more simply in
the untimed model, by using correctness-preserving migration between models in
the hierarchy. Only the timing part of the specification need be checked in
the more complex timed model.
- In a dual language system it is possible to consider automated model
checking of finite state systems. Such model checking has been investigated
for the algebra TPCCS [37]. For ATP [99] processes are
translated into timed transition systems [3] which has already
available model checking algorithms (see section on temporal logics).
- In a single language framework both the detailed implementation P of
the system and its abstract specification S are terms of the
process algebra. A bisimulation is then used to show that the implementation is
equivalent to its abstract specification, i.e. P∼S.
Often, the requirement that two specifications be equivalent is too strong. For
example, it may not be necessary to prove two processes equally fast, as
perhaps ``faster'' would be sufficient. On the other hand equivalences are
interesting tools for abstractions as a larger concrete implementation can be
replaced by its smaller high level specification, and vice versa [37].
The approach of using a bisimulation has been successful in the untimed case.
However, some researchers claim that it will not be useful in the timed case
owing to the complexity introduced by the timed constructs [21].
The dual language approach of using a specification language such as temporal
logic, has the advantage of separation of concerns. Each relevant requirement
can be expressed as a separate formula, and each formula can be verified
separately [37].
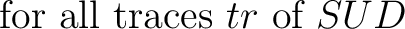 Q means the process P may perform the atomic and
timeless action a and then it behaves like Q. The transition
P
Q means the process P may perform the atomic and
timeless action a and then it behaves like Q. The transition
P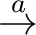 Q means that the process P may idle for d time
units after which it behaves like Q. A time domain is a commutative monoid
(D, + , 0). As D is usually infinite, models of processes are generally
infinitely branching transition systems.
Q means that the process P may idle for d time
units after which it behaves like Q. A time domain is a commutative monoid
(D, + , 0). As D is usually infinite, models of processes are generally
infinitely branching transition systems.
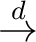 O', A, R',∼'). It must then be
decided how to obtain the operational semantic rules R' and the strong
equivalence ∼' with respect to the labelled transition system.
O', A, R',∼'). It must then be
decided how to obtain the operational semantic rules R' and the strong
equivalence ∼' with respect to the labelled transition system.
 S can
then be constructed. This is the main method used for verification in TCSP.
The TCSP proof system has been used to prove the correctness of control
software for aircraft engines, of realistic telephone switching networks and
of a local area network protocol [
S can
then be constructed. This is the main method used for verification in TCSP.
The TCSP proof system has been used to prove the correctness of control
software for aircraft engines, of realistic telephone switching networks and
of a local area network protocol [