Home

Info.

Article

Products

Stickers

UserGroups

Events

Books

	Linux magazine| LinuxUser| Linux Events| Linux Community| Perl Snapshots		Searches:
			Now order! Abo order Yearly CD 2001

Combinatorial and geometrical counting

LEDA

1. Why does it LEDA give?

• The relevant librettos contained only outlined algorithms. It is a very long way from these descriptions to correct implementations, which treat then also all degenerate cases (with it the so-called cases degenerated are meant) correctly.
• Many companies have at all nobody, these representations sufficiently well understand and select therefore dear trivial solutions.
• It is not worthwhile itself to implement a good algorithm if one must spend too much time and thus money on it and it does not bring anything for other problems. Also therefore many prefer the third-best however only times more inexpensive solution.
• That the algorithm really which brings and that we can use it more than once, we see only if we tried it out. As pure experiment is however too expensive.

Now one could conclude, there would at all be no implementations for algorithms from this forschungsgebiet. Far been missing. To many projects or theses (diploma) also the conversion of cleverer solution strategies belongs. There again and again those emerge in principle same data structures in completely easily modified form. And each student had programmed his own version of for example binary trees. On request, why like that is, we received into the following answers:

• Me is not clear at all, which does the program of another exactly.
• Before I change another program laboriously, I program it rather again.
• I did not want to rely on the fact that the program of another is correct.

Combinatorial and geometrical counting represents one of the central areas of computer science. For this reason also most university curricula contain courses over data structures and efficient algorithms. Typical objects of this area are graphs, consequences, dictionaries, trees, shortest ways, rivers, illustrations, points, segments, lines, convex coverings and Voronoi diagrams (for the less usual terms it gives in the appendix an explanation); it forms the basis for such Anwendungungen like discrete optimization, planning, traffic control, CAD, diagram and much more besides. The fact that there was no standard library for data structures and algorithms stood for statistics (SPSS) in clear contrast to other disciplines as for example, numerical analysis (LINPACK, ICE LUGGAGE), symbolic counting (MAPLE, MATHEMATICA) or linear programming (CPLEX).

The absence of a library had extremely negative effects in the past on the use of the area for entire computer science. The constantly repeating new implementing of fundamental data structures and algorithms obstructs the progress not only within the research, but above all also in the free economy. We already called the reasons for it.

But on what now the absence of a library of efficient algorithms and data structures is to be led back? One of the largest differences between combinatorial or geometrical counting and other areas such as statistics, numerical analysis and linear programming is the use of complex data types. While the types built into programming languages are normally sufficient like whole or real numbers, vectors and stencils for other areas, like already suggested combinatorial and geometrical counting is based particularly on types such as cellars, queues, lists, dictionaries, consequences, graphs, points, lines and convex coverings. It requires therefore a programming environment, which makes all these types available. With the introduction of object-oriented programming such became possible an extension in efficient and elegant way.

In the year 1989 we could begin therefore with the LEDA project. The goal was thus to develop a library of the data types and algorithms for combinatorial and geometrical counting.

In the available article I would like to obtain a rough overview of this library, by calling the main characteristics and on the basis simple examples illustrate the use of the different parts. Into later expenditures I will continue to go into the detail and the underlying concepts of the different data structures as well as the conversion by programming to LEDA will more exactly describe. Parts of the text will orient themselves at different chapters of the book LEDA , Platform for Combinatorial and Geometric Computing of Kurt flour horn and Stefan close, which with Oxford University press will appear.

2. What now is LEDA?

• LEDA makes a considerable number of data types and algorithms available in a form, which permits it also to non--experts to use her. This collection contains most of the data types and algorithms, which are described in librettos of this area: Cellar, queues, lists, quantities, dictionaries, arranged, nondirectional and planar graphs, lines, points and levels; in addition many algorithms of the graph and netzwerktheorie as well as algorithmic geometry come.
• LEDA is written in C++. The data types and algorithms are stored in it as by-set object modules. This leads together with the fact that due to the large expression strength of LEDA application programs are short, to short translation times.
• LEDA gives a precise and readable specification for everyone of the mentioned data types and algorithms. The specifications are briefly (usually not longer than a side), generally (they permit different implementations) and abstract (implementation details are hidden).
• Many data types in LEDA are parameterized; for example the type of dictionary for arbitrary key and information types functions. A special object D with type of key stringer and type of information int can e.g. through

  dictionary < stringer, int > D

  are defined.

• LEDA contains the most efficient implementations, which admits for its data types is. For many of the types the user between different implementations can select, for example off-rise, BB[a] trees, dynamic perfect Hashing or Skiplisten for dictionaries. So realized for example the definition

    _ dictionary<string, int, skip_list > D  

  a dictionary by Skiplisten.
• As is still described later, that is important access over a position for many efficient data structures. LEDA uses a new Item concept around positions to treat abstractly to be able.
• LEDA contains a comfortable type graph. This offers standard iterations like ` for all knots v of a graph G does ' (forall_nodes(v, G)do or ` for all neighbours w of v ' (forall_adj_nodes(w, v)Knots and edges can be added or deleted at will. Also fields and stencils are made available, which can be indicated with the knots or edges. With the help of the data type graph can the programs for the release from graph problems be nearly exactly the same written, how they are to be normally found in librettos. I would like to stress that all programs printed here are translation and executable. The goal is the equation ` algorithm + LEDA = program '.
• Many geometrical algorithms use arbitrarily exact arithmetic and are therefore free from rounding errors. Beyond that they come with all cases degenerated clearly.
• LEDA supports variety of ranges of application. Thus it was already used in as different areas as code optimizing, VLSI Design, robot movement planning, traffic planning, machine learning and algorithmic biology.
• There is its own Windowsklasse, which permits it to program platform-independently own demos and graphic input and output.
• LEDA is meanwhile applicable on a large number of surfaces (beside Linux on all Unix computers, OS/2, Windows NT and 95 as well as on MSDOS with all usual compilers).

2.1 Worte zählen

Das vollständige Programm ist in Abbildung 1 zu sehen:

#include <LEDA/d_array.h>

int main(int argc, char** argv)
{ 
  d_array<string,int> N(0);
  string s;
  while (cin >> s) N[s]++;
  forall_defined (s,N)
    cout << s << " " << N[s] << endl;
 }

Abb. 1: Ein Programm, das die Anzahl der Vorkommen jedes Strings in einer Folge von Strings zählt.

Es beginnt mit einer #include Anweisung für Dictionary Arrays. In der ersten Zeile des Hauptprogramms definieren wir ein Dictionary Array N mit Indextyp string und Elementtyp int und initialisieren alle Einträge des Array auf 0. (Die Implementierung von d_array speichert alle Einträge, die von Null verschieden sind, in einem balancierten Suchbaum mit Schlüsseltyp string). In der zweiten Zeile definieren wir einen String s. Die dritte Zeile verrichtet die ganze Arbeit. Der Ausdruck (cin >> s) gibt true zurück, wenn der Eingabestrom nicht leer ist, andernfalls gibt er false zurück. Im ersteren Fall wird der erste String vom Eingabestrom entfernt und der Variablen s zugewiesen. Dann wird der Eintrag N[s] des Arrays N inkrementiert. Die Iteration forall_defined(s, N) in der letzten Zeile weist nacheinander alle Strings, für die auf N während der Ausführung des Programms zugegriffen wurde, der Variablen s zu. All diese Strings werden zusammen mit der Häufigkeit ihres Auftretens auf die Standardausgabe ausgegeben.

2.2 Kürzeste Wege in Graphen

Abb. 2: Ein Graph mit Kantenbeschriftungen. Diese geben die Reisezeit (in Minuten) über die jeweilige Kante an. Die kürzeste Reisezeit von Knoten s zu Knoten c beträgt 4 Minuten.

Dijkstra [Dij59] hat einen einfachen Algorithmus gefunden, der dieses Problem löst. Zu jedem Zeitpunkt während der Ausführung des Algorithmus gibt es eine Menge S, Teilmenge von V, von Knoten, für die die minimale Reisezeit bereits bekannt ist, während für alle anderen Knoten lediglich eine obere Schranke für die Reisezeit bekannt ist, d.h., eine Zeitspanne, in der man die Strecke auf jeden Fall bewältigen kann, die jedoch nicht notwendigerweise minimal ist.

Für jeden Knoten v bezeichnen wir mit dist[v] die kürzeste bisher bekannte Reisezeit von s nach v. Anfangs ist dist[s] = 0, dist[v] = unendlich für jeden Knoten v != s, und S = leere Menge. In jedem Schritt wählen wir einen Knoten u aus V-S mit dem kleinsten Wert dist[u] (am Anfang ist u = s) und fügen ihn zu S. Für jede von u ausgehende Kante e = (u, w) setzen wir dist[v] auf den Wert dist[u] + cost[e], wenn dieser Wert kleiner ist als der aktuelle Wert von dist[v]. In unserem Beispiel ist s der erste Knoten, der zur Menge S kommt. Wenn dies geschieht, wird dist[a] auf 2 gesetzt und dist[c] auf 6. Dann fügen wir a zu S, dist[b] wird auf 3 gesetzt und dist[c] wird auf 5 erniedrigt, ... . Die Korrektheit dieses Algorithmus soll hier nicht bewiesen werden (Beweisidee: man zeigt, daß für alle Knoten v der Wert von dist[v] immer die kürzeste Reisezeit von s nach v entlang eines Pfades angibt, dessen Knoten alle mit Ausnahme des Endknotens zu S gehören). Wie können wir nun den Knoten in V-S mit dem kleinsten dist-Wert schnell finden? Eine geeignete Datenstruktur ist eine Warteschlange. Abbildung 3 zeigt die LEDA-Implementierung von Dijkstras Algorithmus.

#include <LEDA/graph.h>
#include <LEDA/node_pq.h>

void DIJKSTRA(const graph& G, node s, 
              const edge_array<int>& cost, 
              node_array<<nt>& dist)
{ 
  node_pq<int>  PQ(G);
  node v;                                                                    
  forall_nodes(v,G) { 
    dist[v] = (v == s) ? 0 :MAXINT; 
    PQ.insert(v,dist[v]);
  }
  while (! PQ.empty()) { 
    node u = PQ.del_min();
    edge e;
    forall_adj_edges(e,u) { 
      v = target(e);                                                      
      int c = dist[u] + cost[e];                                              
      if (c < dist[v]) { 
        PQ.decrease_p(v,c);
        dist[v] = c;                                                     
      }                                                                 
    }                                                                    
  } 
}

Abb. 3: Dijkstras Algorithmus für das Problem der Berechnung aller kürzesten Wege von einem Knoten aus.

Neben Graphen benutzt er node_array (Knotenfeld), edge_array (Kantenfeld) und node_pq (Knoten-Warteschlange). Knoten- und Kantenfelder sind Felder, die mit Knoten bzw. Kanten indiziert sind. Man kann sie also benutzen, um an die abstrakten Graphenelemente Daten zu schreiben und ihnen somit eine Bedeutung zu geben. Wir benutzen ein edge_array<int> cost, um die Reisezeiten entlang der Kanten zu speichern, ein node_array<int> dist um die minimale Reisezeit zu jedem Knoten zu speichern und eine node_pq<int> PQ(G). An dem Parameter G in der Definition von PQ erkennt LEDA, daß G der zugrundeliegende Graph ist. Die Knoten-Warteschlange PQ enthält stets alle Knoten von G, die in V-S liegen, zusammen mit ihren aktuellen dist-Werten. Am Anfang werden alle Knoten in PQ eingefügt. Bei jeder Iteration wird der Knoten mit dem kleinsten zugehörigen Wert aus PQ gelöscht (u = PQ.del_min()) und alle von u ausgehenden Kanten e werden überprüft (forall_adj_edges(e, u)). Falls notwendig wird dabei der dist-Wert des Zielknotens verringert (PQ.decrease_inf(v, c)).

Wir möchten besonderes auf die große ähnlichkeit zwischen dem LEDA Programm und der Beschreibung des Algorithmus hinweisen. Die gleiche ähnlichkeit ist bei den meisten Graphenalgorithmen anzutreffen. In diesem Sinne erfüllt LEDA die Gleichung ``Algorithmus + LEDA = Programm''.

Erwähnenswert ist sicher auch, daß ein Programmierer von Dijkstras Algorithmus nichts über die innere Funktionsweise von Graphen und Knoten-Warteschlangen zu wissen braucht. Die Kenntnis der relevanten Seiten im Handbuch genügt vollkommen. Abbildung 4 zeigt die Handbuchseite für Knoten-Warteschlangen (node_pq).

Im letzten Abschnitt gibt diese Seite die Laufzeiten der verschiedenen Operationen für Warteschlangen an: konstante Zeit für insert, empty und decrease_inf, und logarithmische Zeit für del_min. In einem Graph mit n Knoten und m Kanten benötigt Dijkstras Algorithmus n inserts, empty-Tests und del_mins und höchstens m decrease_infs. Seine Laufzeit ist deshalb proportional zu m + n * log n.

Node priority queues (node_pq)

1. Definition

An instance Q of the parametrized data type 
node_pq<I> is a set of pairs (v,i), where
v is a node of some graph G and i belongs to some linearly
ordered type I; i is called the information associated with
node v. For any node v of G there can be at most one pair (v, )
in Q.

2. Creation

node_pq<I> Q(G);
 
creates an empty instance Q of type  node_pq<I> for the 
nodes of graph G.


3. Operations 

void   Q.insert(node v,  I i)         adds the node v with information i to Q. 
                                      Precondition: There is no pair (v, ) in Q.

I      Q.inf(node v)                  returns the information of node v.

bool   Q.member(node v)               returns true if (v,i) in Q for some i, 
                                      false otherwise.

void   Q.decrease_inf(node v, I i)    makes i the new information of node v.
                                      Precondition: i <= Q.inf(v)).

node   Q.find_min()                   returns a node with the minimal 
                                      information (nil if Q is empty).

void   Q.del(node v)                  removes the pair (v, ) from Q.

node   Q.del_min()                    removes a node with minimal information 
                                      from Q and returns it (nil if Q is empty).

int    Q.size()                       returns the number of pairs in Q.

void   Q.clear()                      makes Q the empty node priority queue.

bool   Q.empty()                      returns true if Q is the empty node
                                      priority queue, false otherwise.


4. Implementation

Node priority queues are implemented by fibonacci heaps and node arrays.
Operations insert, del_node, del_min take time O(log n), find_min, decrease_inf,empty take time O(1) and clear takes time O(m), where m is the size of Q. The 
space requirement is O(n), where n is the number of nodes of G.

Abb. 4: Die Handbuchseite für Knoten-Warteschlangen.

2.3 Konvexe Hüllen

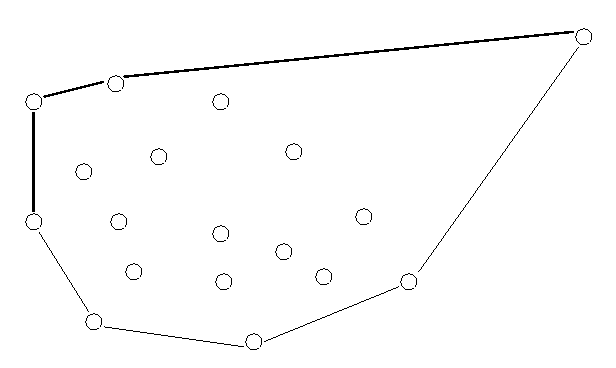
Abb. 5: Die konvexe Hülle einer Punktemenge in der Ebene. Die obere Hülle ist dick gezeichnet.

Die konvexe Hülle ist eine der grundlegenden Strukturen in der algorithmischen Geometrie. Sie wird bei der Bildverarbeitung oder Mustererkennung oft als eine Annäherung an die Form einer Punktmenge benutzt. Wir erklären im folgenden, wie wir die konvexe Hülle berechnen, wenn die Punktmenge gegeben ist: wir beschränken uns der Einfachheit halber auf die sogenannte obere Hülle. Wenn wir die konvexe Hülle nämlich durch eine Gerade durch den Punkt der am weitesten links und den Punkt der am weitesten rechts liegt, durchschneiden, zerteilen wir sie in die obere und die untere Hülle von L (siehe Abbildung 5). Dabei ist ein Punkt p links von einem Punkt q, wenn entweder die x-Koordinate von p kleiner ist als die von q ist oder wenn die x-Koordinaten der beiden Punkte gleich sind und die y-Koordinate von p ist kleiner ist als die von q.

Wir berechnen die obere Hülle einer Punktmenge L wie folgt: Zuerst sortieren wir die Menge L gemäß der oben definierten Links-Rechts Reihenfolge ihrer Punkte. Sei p_1, p_2, ... , p_n die gemäß dieser Reihenfolge aufsteigend sortierte Folge. Wir konstruieren die obere Hülle der Punkte p_1, ... , p_i inkrementell für alle i, 1 <= i <= n. Die Initialisierung ist einfach. Die obere Hülle von p_1 ist p_1. Setzen wir nun voraus, daß die obere Hülle der Punkte p_1, ... , p_i bereits berechnet ist und daß wir den Punkt p_i+1 abarbeiten. Wenn p_i = p_i+1, dann ist nichts zu tun. Wenn aber p_i != p_i+1, dann löschen wir den jeweils letzten Punkt der aktuellen oberen Hülle, solange diese mindestens aus zwei Punkten besteht und mit dem neuen Punkt p_i+1 keine Rechtskurve bildet (siehe Abb. 6).

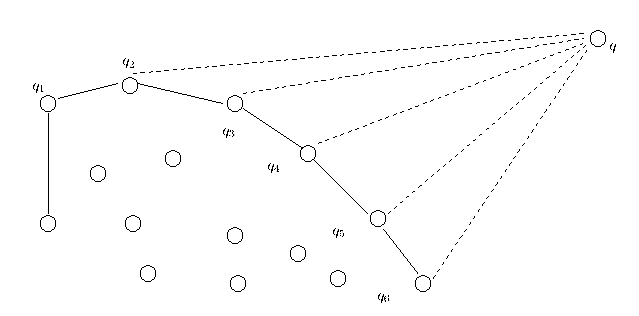
Abb. 6: Die oberer Hülle nach dem Abarbeiten aller Punkte außer q. Wenn der Knoten q hinzugefügt wird, werden die letzten vier Punkte der aktuellen Hülle gelöscht, weil (q_i, q_i+1), q für 2 <= i <= 5 keine Rechtskurve bildet.

Dann addieren wir p_i+1 zur oberen Hülle; damit ist der Iterationsschritt abgeschlossen. Abbildung 7 zeigt die LEDA Implementierung von diesem Algorithmus. Wegen der schon erwähnten großen ähnlichkeit zwischen der algorithmischen Beschreibung und dem LEDA Programm sind nur wenige zusätzliche Worte notwendig, um das Programm zu erklären: L.sort() sortiert die Liste L gemäß einer vordefinierten Ordnung auf ihren Elementen. Für Punkte ist dies die bereits erwähnte Links-Rechts Reihenfolge. L.pop() löscht das erste Element der Liste und gibt es zurück. Uh.append(p) hängt den Punkt p an die Liste Uh an, L.empty() gibt true zurück, wenn L leer ist, Uh.length() gibt die Länge der Liste Uh zurück, und Uh.Pop() löscht das Element, das sich jeweils am Ende der Liste Uh befindet. In LEDA wird eine Liste als eine Folge sogenannter Items (mit dem Typ list_item) betrachtet, wobei jedes dieser Items ein Element der Liste enthält. Uh.last() gibt das letzte Item der liste Uh zurück und für ein Item it kann mit Uh[it] auf den Inhalt des Items zugegriffen werden. Das Vorgänger-Item von it in der Liste Uh erhält man mit Uh.pred(it).

#include <LEDA/list.h>
#include <LEDA/plane.h>

list<point> u_hull(list<point> L)
{ L.sort();  // into left-to-right order
  list<point> Uh;
  point p = L.pop();
  Uh.append(p);
  while (!L.empty())
  { point q = L.pop();  // deletes the first element from L
    if (p == q) continue;
    list_item it = Uh.last();
    while (Uh.length() >= 2 && 
           right_turn(Uh[Uh.pred(it)],Uh[it],q))
    { Uh.del_item(it);  // deletes the last element from Uh
      it = Uh.last();
     }
    Uh.append(q);
    p = q;
   }
  return Uh;
}

Es gibt noch eine weitere interessante Beobachtung bei dem Programm zur Berechnung der konvexen Hülle. Ein Punkt in LEDA kann beliebige rationale Koordinaten enthalten und alle Prädikate werden exakt (d.h. mit genauer rationaler Arithmetik) ausgerechnet. Beachten Sie auch, daß das Programm mehrfaches Auftreten des gleichen Punktes ebenso korrekt verarbeitet wie kollineare Punkte (solche Situationen werden degenerierte Fälle genannt). Es ist vorgesehen, daß alle geometrischen Algorithmen in LEDA mit allen degenerierten Fällen zurecht kommen und momentan trifft dies bereits für viele zu. Weitere Details hierzu können in [BMS94a], [BMS94b] und [MN94b] nachgelesen werden.

2.4 Grafik

#include <LEDA/window.h>

int main(int argc, char** argv)
{ 
  window W;
  list<point> L;
  point p;
  while (W >> p)
  { 
    L.append(p);
    W.draw_point(p);
   }
  W.draw_polygon(u_hull(L));
  W.read_mouse
}

Abb. 8: Ein Programm, das den Algorithmus für die obere Hülle und die Schnittstelle zu XWindows illustriert.

Das Programm liest eine Folge von Punkten ein, gibt sie in einem Fenster aus und zeichnet ihre obere Hülle als Linienzug. Wieder reichen wenige Erklärungen aus: Die Definition window W definiert ein grafisches Fenster und öffnet es für die Mauseingabe. Durch Drücken der linken Maustaste gibt man einen Punkt ein (W >> p); beim Betätigen der rechten Maustaste wird W >> p als false ausgewertet. Der Punkt wird an die Liste L gehängt und im Fenster W gezeigt. Danach wird die obere Hülle berechnet und als Linienzug gezeichnet. Abbildung 9 zeigt ein Beispiel.

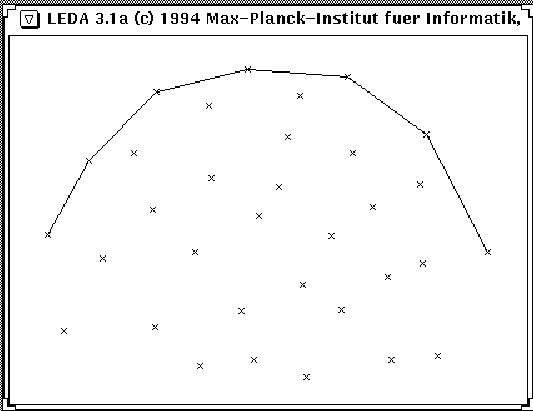
Abb. 9: Eine Ausgabe des Programms zum Berechnen der oberen Hülle.

3. Was ist alles drin in LEDA?

Die Basisdatentypen sind Strings, Listen, Schlangen, Keller, Felder, Partitionen und Bäume.

Die Zahlentypen umfassen sowohl die eingebauten Typen (int, float, double) als auch Typen mit beliebiger Genauigkeit (integer, real). Der Typ integer entspricht der Menge der ganzen Zahlen im mathematischen Sinne, also ohne Beschränkung der Zahlengröße (wenn man mal von der Speichergröße absieht); real entspricht der Klasse der floating point Zahlen mit Mantisse und Exponent in beliebiger Genauigkeit. Es gibt auch Vektoren und Matrizen für all diese Zahlentypen.

In der dritten Gruppe gibt es Warteschlangen, Wörterbücher, Wörterbuch- und Hashingfelder, Sortierte Folgen und persistente Wörterbücher.

Der Graphenteil bietet verschiedene Arten von Graphen: gerichtete Graphen, ungerichtete Graphen und planare Graphen. Darüber hinaus gibt es noch weitere Datenstrukturen auf Graphen wie etwa Felder, die mit Knoten oder Kanten indiziert sind, Warteschlangen für Knoten, Knotenpartitionen und andere. Zusätzlich ist eine große Anzahl von Algorithmen auf Graphen und Netzwerken verfügbar: Kürzeste Wege, zweifache Zusammenhangskomponenten, starke Zusammenhangskomponenten, transitive Hülle, topologisches Sortieren, ungewichtetes und gewichtetes bipartites Matching, ungewichtetes allgemeines Matching, Netzwerkfluß, Netzwerkfluß mit minimalen Kosten, Planaritätstest, planare Einbettung, minimaler aufspannender Baum, usw.. Dem LEDA-Handbuch [NU95] kann man entnehmen, was es sonst noch alles gibt.

4. Wie ist es gemacht?

Alle Datentypen in LEDA sind durch die asymptotisch effizienteste Implementierung realisiert, die bekannt ist. Für viele Datentypen werden verschiedene Implementierungen zur Verfügung gestellt. Beispielsweise kann der Benutzer bei den Wörterbüchern unter ab-Bäumen, AVL-Bäumen, BB[a]-Bäumen, Rot-Schwarz-Bäumen, Skiplisten und randomisierten Suchbäumen wählen (all dies sind Datenstrukturen, die im wesentlichen das Einfügen, Löschen und schnelle Auffinden von Daten gut unterstützen). Der Mechanismus zum Auswählen einer anderen Implementierung ist ziemlich bequem. Wenn man zum Beispiel die Definition des Wörterbuchfeldes N im Wörterzähl-Programm durch _d_array<string, int, skip_list> N(0) ersetzt, werden automatisch Skiplisten benutzt.

Abstrakte Datentypen verstecken die Implementierungsdetails einer Datenstruktur. Allerdings kann die Abstraktion, wenn sie nicht sorgfältig durchgeführt wird, auch einen Effizienzverlust mit sich bringen, wie folgendes Beispiel erläutert. Ein Wörterbuch mit Schlüsseltyp K und Informationstyp I wird gewöhnlich als Abbildung von K nach I betrachtet. Nehmen wir nun an, jemand möchte zuerst auf die Information zugreifen, die zu einem Schlüssel k gehört, dann diese Information verändern, um schließlich die neue Information an den Schlüssel k zu binden. Ist ein Wörterbuch auf herkömmliche Weise definiert, werden dabei zwei Suchvorgänge notwendig: Beim ersten Suchen werden der Schlüssel k und die dazugehörige Information lokalisiert. Der zweite Suchvorgang lokalisiert k noch einmal und assoziiert eine neue Information mit k. Ein direkter Zugriff auf die Datenstruktur könnte jedoch die zweite Suche sparen. Man merkt sich einfach einen Zeiger auf die Position des Schlüssels k in der Datenstruktur und ersetzt den zweiten Suchvorgang durch direkten Zeigerzugriff.

In LEDA wurde ein neues Item-Konzept eingeführt, um die durch die Abstraktion eingeführte Ineffizienz zu umgehen. Ein Wörterbuch wird als eine Sammlung von items (mit dem Typ dic_item) betrachtet, von denen jedes einen Schlüssel und eine Information enthält. Die Schlüssel, die mit verschiedenen Informationen assoziiert sind, sind verschieden. Eine Suche in einem Wörterbuch nimmt einen Schlüssel und gibt ein Item zurück (und nicht die darin enthaltene Information). Auf die Information kann nun über dieses Item zugegriffen werden. Das Wesentliche dabei ist, daß man das Item speichern und später direkt über dieses Item zugreifen kann, ohne es erneut suchen zu müssen.

Auf diese Weise stellen Items die Abstraktion einer Position in einer Datenstruktur dar. Sie ermöglichen einerseits Effizienz und erlauben andererseits vollständige Verkapselung der zugrundeliegenden Datenstruktur. Unserer Meinung nach ist das Item-Konzept ein Schlüsselfaktor für die Effizienz von LEDA. Weitere Informationen dazu finden sie im LEDA-Handbuch [NU95] und in [MN92].

Natürlich müssen wir einen Preis für die Universalität von LEDA zahlen. Dr. Ullrich Lauther von der Siemens AG in München [Lau92] hat intensive Vergleiche zwischen mit LEDA implementierten Graphen- und Netzwerkalgorithmen und von Hand in C geschriebenen durchgeführt. Er erklärt, die LEDA Versionen seien um einen Faktor zwischen 2 und 10 (normalerweise etwa 4) langsamer als seine eigenen Versionen und benötigten zwischen 2 und 3,5 mal soviel Speicherplatz. Wir glauben, daß man dies in Anbetracht der Bequemlichkeit, die LEDA bietet, durchaus akzeptieren kann. Als Reaktion auf Lauthers Bericht haben wir mittlerweile einige grundlegenden Datenstrukturen (in erster Linie graph) neu implementiert, wodurch der Overhead auf einen Faktor von etwa 2 reduziert wurde.

5. Sind die Programme korrekt?

• Wir gehen von korrekten Algorithmen aus (die Algorithmenforschung legt glücklicherweise großen Wert auf Korrektheit und Analyse).
• Die neueren Programme dokumentieren wir ausführlich, siehe z.B. [MN94a], [MZ93].
• Wir testen unsere Programme intensiv und die große Nutzergemeinde von LEDA tut es auch.
• Wir entwickeln Prüfprogramme, die die Ausgaben unserer Programme automatisch verifizieren.

1992 bekamen wir einen planaren Graphen zugesandt, den unser Programm für nicht planar erklärt hatte. Bei der Reimplementierung des Algorithmus [MMN93] erkannten wir, daß wir nur dann Vertrauen in die Korrektheit unserer Implementierung haben könnten, wenn diese ihre Antwort belegen würde.

Die neue Implementierung tut daher folgendes: Wenn der Eingabegraph planar ist, dann liefert das Programm eine planare Einbettung, und wenn der Eingabegraph nicht planar ist, dann liefert das Programm einen sogenannten Kuratowski-Untergraphen, der die Nichtplanarität bezeugt (es gibt einen mathematischen Beweis dafür, daß nicht-planare Graphen einen solchen Graphen als Untergraphen besitzen müssen). Ein Nutzer der Neuimplementierung muß nun nichts mehr glauben, er erhält vielmehr für jeden Eingabegraphen einen Beweis für die Korrektheit der Ausgabe. Diejenigen Leser, die Zugang zur LEDA-Bibliothek haben, sollten die Vorführung plan_demo ausprobieren.

Dabei wird auffallen, daß der Planaritätstest und das Erstellen der Zeichnung sehr schnell funktionieren (die entsprechenden Programme laufen in Linearzeit), daß aber das Finden der Kuratowskigraphen vergleichsweise lange dauert (die Laufzeit ist quadratisch). Wir haben auch für das letztere Problem jüngst einen Linearzeitalgorithmus gefunden, aber noch nicht implementiert [HMN96].

7. LEDA im Internet

mailto:leda@mpi-sb.mpg.de

weiterhin eine World Wide Web Homepage

http://www.mpi-sb.mpg.de

eine newsgroup

comp.lang.c++.leda und schließlich eine ftp -Adresse, wo man LEDA erhalten kann.

ftp://ftp.mpi-sb.mpg.de/pub/LEDA.

Die Benutzung von LEDA für akademische Forschung und Lehre ist kostenlos. Kommerzielle Interessenten sollten sich die entsprechenden Seiten im WWW ansehen oder sich an obige Email-Adresse wenden.

8. Eine kurze Nachbetrachtung

Ich sollte darauf hinweisen, daß LEDA nicht die einzige Bibliothek für Datenstrukturen ist. Andere sind [GOP90], [Boo87] ([Loc94] gibt einen Überblick) und die Standard Template Library (STL). Die Haupteigenschaft, die LEDA von den anderen Bibliotheken unterscheidet ist ihr Umfang. Keine andere Bibliothek enthält soviele Datentypen und Algorithmen aus dem Gebiet des kombinatorischen und geometrischen Rechnens.

Anhang

degeneriert

Man spricht insbesondere bei geometrischen Problemen von allgemeiner Lage der Eingabe, wenn die Objekte in gewissen Sinne zufällig verteilt sind. Wenn man z.B. drei Punkte in der Ebene zufällig auswählt, erwartet man, daß sie nicht auf einer Linie liegen. Tun sie es doch, dann redet man von einem degenerierten Fall. Diese Fälle sind für die Algorithmen meistens die schwierigen und bei den Formulierungen in den einschlägigen Büchern wird in der Regel allgemeine Lage vorausgesetzt.

Graph

Das ist eine abstraktes Gebilde, das aus einer Menge V von Knoten und E von Kanten (Verbindungen zwischen den Knoten, auch als Knotenpaare (Anfangsknoten, Endknoten) zu betrachten) besteht. Viele Probleme aus der Kombinatorik lassen sich mit Hilfe von Graphen modellieren (man denke z.B. das Berechnen eines Fahrplans auf einem Schienennetz oder das Verschicken von Sendungen im Internet). Es gibt viele spezielle Arten von Graphen mit ganz typischen Eigenschaften.

Einem planaren Graphen kann man z.B. so in der Ebene zeichnen kann, daß sich keine zwei Kanten schneiden, sondern höchstens in ihren Endpunkten berühren (wenn es eben der gleiche Endpunkt ist).

Die Knoten eines bipartiten Graphen kann man so in zwei disjunkte Teilmengen zerlegen, daß alle Kanten Verbindungen zwischen den beiden Teilmengen sind, es also keine Kante innerhalb einer der beiden Mengen gibt.

Matching:

Wenn ein Graph gegeben ist, versteht man unter einem Matching eine Teilmenge der Kanten, so daß kein Knoten zu mehr als eine Kante im Matching (wenn man die Kanten als Knotenpaare interpretiert) gehört. Normalerweise versucht man, für einen gegebenen Graphen ein möglichst großes Matching (viele Kanten) zu finden. Man kann aber auch jeder Kante ein sogenanntes Gewicht (einen Zahlenwert) zuordnen, so daß manche Kanten wichtiger sind als andere. Man sucht dann ein möglichst schweres Matching.

Netzwerkfluß:

Hierbei betrachtet man einen Graphen gewissermaßen als ein Transportnetz, wo von bestimmten Startknoten zu bestimmten Zielknoten eine Substanz über die verbindenden Pfade verschickt werden soll. Den Kanten wird in der Regel eine maximale Kapazität und ein Kostenwert zugeschrieben. Man möchte nun z.B. möglichst viel der betreffenden Substanz verschicken; unter Umständen dies auch noch möglichst billig. Solche Probleme werden von Netzwerkflußalgorithmen gelöst.

persistent:

Damit meinen wir (es gibt andere Definitionen), daß bei einer Datenstruktur nicht nur der letzte Zustand sondern auch alle vorhergehenden noch vorhanden sind und ich auch mit irgendeiner Datenstruktur aus der Vergangenheit (z.B. vor den letzten 10 Instruktionen) weiterarbeiten kann. Jede Veränderung schafft gewissermaßen eine neue Version der Struktur und alle Versionen bleiben immer verfügbar.

Voronoidiagramm:

Sei eine Menge von Orten und Gegenständen in der Ebene gegeben. Dann versteht man unter einem zweidimensionalen Voronoidiagramm eine Zerlegung der Ebene in diskunkte Gebiete, so daß jedes der Gebiete eines der Objekte enthält und zu jedem Punkt des Gebietes das darin enthaltene Objekt das nächste von allen Objekten ist (wobei nächstes geeignet definiert werden muß, z.B. normaler Luftlinienabstand sein kann). Wenn ich also das Voronoidiagramm einer Stadt bzgl. der dort vorhandenen Kneipen habe und ich weiß, in welchem Gebiet ich mich befinde, dann ist die in diesem Gebiet befindliche Kneipe die nächste.

Wörterbuch:

Das ist eine Menge von Behältern (items), von denen jeder ein Schlüsselelement aus einer sortierbaren Menge (z.B. ein Wort aus der deutschen Sprache) und ein Informationselement aus einer anderen Menge (etwa die entsprechende Vokabel aus dem französischen) enthält. Es können neue Paare hinzugefügt, alte gestrichen oder geändert, es kann nach Inhalten gesucht werden und einiges mehr.

Zusammenhangskomponenten:

Einen Graph kann man in Zusammenhangskomponenten (ZK) zerlegen. Eine solche Komponente besteht aus einer Menge von Knoten, so daß es zwischen beliebigen zwei Knoten aus dieser Menge immer einen Pfad von Kanten gibt, der sie verbindet. Es gibt dann keine Verbindungen von einer ZK zu einer anderen.

Bibliographie

[AHU83]
A.V. Aho, J.E. Hopcroft, and J.D. Ullman.
Data Structures and Algorithms.
Addison-Wesley Publishing Company, 1983.

[BMS94a]
Ch. Burnikel, K. Mehlhorn, and S. Schirra.
On degeneracy in geometric computations.
In Proc. SODA 94, 16--23, 1994.

[BMS94b]
Ch. Burnikel, K. Mehlhorn, and St. Schirra.
How to compute the Voronoi diagram of line segments: Theoretical
and experimental results.
In LNCS, Proceedings of ESA'94, volume 855, 1994.

[Boo87]
G. Booch.
Software Components with Ada.
Benjamin/Cummings Publishing Company, 1987.

[CLR90]
T.H. Cormen, C.E. Leiserson, and R.L. Rivest.
Introduction to Algorithms.
MIT Press/McGraw-Hill Book Company, 1990.

[Dij59]
E.W. Dijkstra.
A note on two problems in connexion with graphs.
Numer. Math., 1:269--271, 1959.

[GOP90]
K.E. Gorlen, S.M. Orlow, and P.S. Plexico.
Data Abstraction and object-oriented programming in C++.
John Wiley and Sons Ltd., 1990.

[HMN96]
C. Hundack, K. Mehlhorn, and S. Näher.
A Simple Linear Time Algorithm for Identifying Kuratowski Subgraphs of 
Non-Planar Graphs, to appear, 1996

[Kin90]
J.H. Kingston.
Algorithms and Data Structures.
Addison-Wesley Publishing Company, 1990.

[Lau92]
U. Lauther.
Untersuchung der library of efficient data types and algorithms
(LEDA).
Technical report, Siemens AG, ZFE, München, 1992.

[Loc94]
N. Locke.
C++ FTP Libraries.
C++ Report, 6(2):61--65, 1994.

[Meh84]
K. Mehlhorn.
Data Structures and Efficient Algorithms.
Springer Verlag, 1984.

[MMN93]
K. Mehlhorn, P. Mutzel, and St. Näher.
An implementation of the Hopcroft and Tarjan planarity test and
embedding algorithm.
Technical Report MPI--I--93--151, Max--Planck--Institut für
Informatik, Saarbrücken, 1993.

[MN92]
K. Mehlhorn and St. Näher.
Algorithm design and software libraries: Recent developments in the
LEDA project.
In Algorithms, Software, Architectures, Information Processing
92, volume 1. Elsevier Science Publishers B.V., 1992.

[MN94a]
K. Mehlhorn and S. Näher.
Implementation of a sweep line algorithm for the segment intersection
problem.
Technical Report MPI-I-94-160, Max-Planck-Institut für Informatik,
Saarbrücken, 1994.

[MN94b]
K. Mehlhorn and St. Näher.
The implementation of geometric algorithms. 
IFIP94, to appear, 1994.

[MNSSSSU96]
K. Mehlhorn, S. Näher, T. Schilz, S. Schirra, M. Seel, R. Seidel, and Ch. Uhrig.
Checking Geometric Programsor Verification of Geometric Structures.
Computational Geomtry, to appear, 1996.

[MZ93]
M. Müller and J. Ziegler.
An implementation of a convex hull algorithm.
Technical Report MPI-I-94--105, Max-Planck-Institut für Informatik,
Saarbrücken, 1993.

[NU95]
St. Näher and Ch. Uhrig.
LEDA manual.
Technical Report MPI-I-95-1-02, Max-Planck-Institut für Informatik,
1995.

[NH93]
J. Nievergelt and K.H. Hinrichs.
Algorithms and Data Structures.
Prentice Hall Inc., 1993.

[O'R94]
J. O'Rourke.
Computational Geometry in C.
Cambridge University Press, 1994.

[Sed91]
R. Sedgewick.
Algorithms.
Addison-Wesley Publishing Company, 1991.

[Tar83]
R.E. Tarjan.
Data Structures and Network Algorithms, volume 44.
CBMS-NSF Regional Conference Series in Applied Mathematics, 1983.

[Wyk88]
C.J. van Wyk.
Data Structures and C programs.
Addison-Wesley Publishing Company, 1988.

[Woo93]
D. Wood.
Data Structures, Algorithms, and Performance.
Addison-Wesley Publishing Company, 1993.

Der Autor

Christian Uhrig ist Mitarbeiter am Max Plank Institut für Informatik und dort unter anderem für das LEDA-Projekt verantwortlich. Daneben ist er auch Geschäftsführer der LEDA Software GmbH, die eine kommerzielle Version von LEDA vertreibt und Support bietet. Zu erreichen ist er unter uhrig@mpi-sb.mpg.de

Copyright © 1996 Linux Magazin