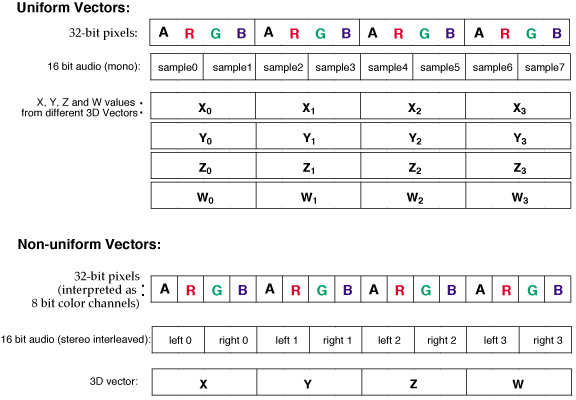
Understanding SIMD

The key to achieving greater performance from the AltiVec unit is to clearly understand the Single Instruction Multiple Data (SIMD) paradigm. Vectors are not best viewed as a 128 bit array of scalars. Nor should each vector be thought of as 16 bytes of random access memory (RAM) that you can read and write data to and from at will. While the vector certainly can be seen and used in this light, member-wise access to vectors typically leads to highly inefficient code.

Instead, the vector is best viewed as a single object, with specific functions to operate on that data. This is an object oriented perspective. Indeed, inspection of the AltiVec C Programming model reveals object oriented programming concepts such as polymorphism and encapsulation at work.

Avoid Member-wise Access to Vectors

The object oriented metaphor works for a variety of reasons. To begin with, encapsulation is tightly enforced by hardware. It is not easy to get individual data into and out of a vector. While it is comparatively easy to load and store entire vectors, member-wise manipulation of data is quite time consuming. (In an ABI that is all about speed, "time consuming" is very close in meaning to "impossible.") For example, if you want to add 1 to just one element in a vector using one of the scalar units, you would have to store that element into memory somewhere. Then you load it back into one of the scalar units, manipulate it, store it back to memory. Finally, load it back into the vector unit and swap the new data into the old vector -- not simple!

Use Uniform Vectors

The second aspect in common between object oriented languages and AltiVec is the importance of remaining faithful to object meaning. For example, suppose you have a Class called Couch_Potato, that embodies the nature and behavior of person who is a television addict. You later discover that you need to make an object to represent a software developer. Even though you may cleverly realize that the behavior of developers and couch potatoes are coincidentally identical in many ways -- each spends many long sedentary hours in a chair in front of a CRT -- you would not make the software developer an instance of the class class Couch_Potato. Doing so would be an example of dishonest use of object meaning. Even though such a "deception" may happen to work now, later on you are likely to run into trouble when the software further develops and differences become more apparent, such as when the software developer asks to be paid! You should, in general, resist the urge to be clever in this way, as you will often find that you are much too clever for your own good.

What does this have to do with vectors? The Single Instruction Multiple Data format takes a single operation and applies it to all of the data in the vector. Implicit in this arrangement is the fact that each element in the vector should have the same meaning. This allows you to apply the same operation to all the elements of the vector at the same time without worrying that the operation is inappropriate or wrong for some of them. This goes beyond having all of the elements of the same type (e.g float). You want to have all of those floats to have the same meaning -- for example the X coordinate for a series of 3D data points. A vector whose elements are all of the same spirit, kind or meaning is called a uniform vector.

Uniform vectors can be used with the AltiVec ABI without having to be selective about which elements are modified. Because the vector elements are identical in meaning, they can be treated identically over the course of the calculation. This allows you to realize true 4, 8 or 16 fold speed increases from vectorization, because you do not have to waste time protecting parts of the vector from certain operations that might do the wrong thing. In addition, code based on uniform vectors tends to look a lot like scalar code. The only difference is that each calculation is applied over 4, 8 or 16 data at once, rather than one at a time. This makes the vector code typically much easier to understand, support and debug. Finally, uniform vectors are conceptually easier to understand because the entire vector can acquire the meaning of the elements within it. A vector full of red channels from a series of pixels conceptually becomes a vector representing the color red for those pixels. You would then have an alpha, red, green and blue vector sitting in your code, instead of four vectors full of assorted color channels. The effort required if, for example, the alpha channel requires special treatment, would be quite trivial.

Non-uniform vectors are those that may contain elements all of the same data type but of different meanings (e.g. a vector containing X, Y, Z and W from a 3D point in space). To the extent that the elements are not identical for the purposes of the calculation, these do not enjoy the advantages noted above for uniform vectors. When working with 3D vectors of this type, we may find that W requires special treatment over the course of a calculation, meaning that we waste a lot of cycles figuring out how to do special things with just the W element. Perhaps we may find that we cant take advantage of optimizations that might rely on the value of only one element in particular. It would be difficult to use just the Y coordinate to determine when a object bounces off the floor, for example. If you did find a way (e.g. by using the NaN method described in Algorithms) you would not be getting four-fold parallelism in the calculation. If instead you use a uniform vector of Y coordinates, you would be able to check four Y coordinates at the same time. To get the same amount of work done with non-uniform vectors, you would have to check four times, once for each Y coordinate in each of four non-uniform vectors. Because the vector elements are not of the same purpose in a non-uniform vector, the vector itself cannot grow to acquire more meaning than a simple vector type such as a vector float. This makes non-uniform vectors typically more abstract and less easy to understand. For all of these reasons, it is generally helpful to design your code to make use of uniform vector types.

Non-uniform types can be a little hard to spot sometimes. For example, if you store a pair of 64 bit integers in a vector, that is a non uniform vector. 64 bit integers are not natively supported by AltiVec. This means that in practice you actually have a vector populated by two high words and two low words or perhaps four different kinds of half-words. Fortunately, non-uniform vectors are often associated with more frequent use of permute instructions (e.g. vec_merge, vec_perm, vec_sld, etc.) Thus, the appearance of many permutes, merges, rotates, etc. in your code is frequently a good sign that you are using non-uniform vectors and furthermore that this could be costing you quite a bit of performance. (By some metrics, permute operations do no real work.) Also, working with non-uniform vectors is usually much more difficult. Consider our sample code that operates on 64 bit integers. Notice how much additional work is required to deal with non-uniform vector types. Some of this code is 2/3 permute. Had we required the user to store their 64-bit integers as a vector unsigned int containing the low word and another vector int containing the high word (or four vectors containing half-words), we might have seen significant performance improvement over the current implementation. The current implementation was chosen because its "standard" data layout makes it somewhat easier to use. That is something that we as an OS provider have to consider. However, in your own application you can store your data however you like, so why not use one that is more conducive to efficient calculation?

Parallelism is the Key

The object metaphor can clearly be taken too far -- it is artificial. The underlying reasons for object oriented design per se are probably code reuse and conceptual simplification of complex problems. (Certainly there are others.) The underlying reason why some of these same principles work for AltiVec is that they enhance parallelism. Violating encapsulation to operate on one element at a time is not operating on many elements in parallel. If all the elements in your vector do not have the same purpose, you will be forced to work on your data in a piecemeal fashion.

Maximizing parallelism maximizes the efficiency of the vector unit. 

Table of ContentsNextPreviousTop of Page